Mỗi cạnh của tam giác ABC đều lớn hơn mỗi cạnh bất kì của tam giác A'B'C'. Có thể khẳng định rằng \(S_{ABC}>S_{A'B'C'}\) được không ? Chứng minh.
Đây là bài toán về chương diện tích ở lớp 8 nhé
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 5 2019
Đáp án là B.
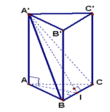
Gọi I là trung điểm BC.
Ta có Δ A B C đều nên A I = A B 3 2 = 2 3 .
A I ⊥ B C A A ' ⊥ B C ⇒ A ' I ⊥ B C
S A ' B C = 1 2 B C . A ' I ⇒ A ' I = 2 S A ' B C B C = 4
A A ' ⊥ ( A B C ) ⇒ A A ' ⊥ A I .
Xét Δ A ' A I vuông tại ⇒ A A ' = A ' I 2 − A I 2 = 2
Vậy V A B C . A ' B ' C ' = S A B C . A A ' = 4 2 3 4 .2 = 8 3
CM
22 tháng 7 2017
Vì
△
A'B'C' đồng dạng
△
ABC nên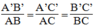 
Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm nên:
A'B'= AB + 10,8cm = 16,2 + 10,8 = 27 (cm)
Ta có: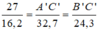 
Suy ra: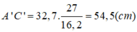 
Suy ra: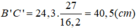 
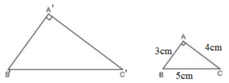
CM
29 tháng 9 2018
Xét ΔABC có: AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ Diện tích tam giác ABC bằng:
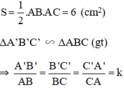
(với k là tỉ số đồng dạng).
Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng
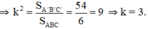
⇒ A’B’ = 3.AB = 3.3 = 9 (cm)
B’C’ = 3.BC = 3.5 = 15 (cm)
C’A’ = 3.CA = 3.4 = 12 (cm)
Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.
CM
17 tháng 9 2019
Vì
△
A'B'C' đồng dạng
△
ABC nên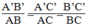 
Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm nên:
A'B'= AB - 5,4 = 16,2 - 5,4 =10,8 (cm)
Ta có: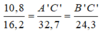 
Suy ra: A'C' = (10,8 . 32,7): 16,2 = 21,8 (cm)
B'C'= (10,8 . 24,3): 16,2 = 16,2 (cm)
CM
16 tháng 7 2017
Chọn D
Diện tích đáy là B = S ∆ A B C = a 2 3 4 .
Chiều cao là h = d((ABC); (A'B'C')) = AA'
Do tam giác ABC là tam giác đều nên O là trọng tâm của tam giác ABC. Gọi I là trung điểm của BC, H là hình chiếu vuông góc của A lên A'I ta có:
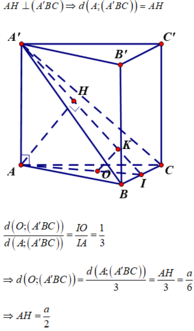
Xét tam giác A'AI vuông tại A ta có:
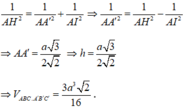
có thể khẳng định
tại sao lại thế