Tính diện tích của tứ giác có độ dài các cạnh lần lượt là 12,5; 41,7; 4,5; 47
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
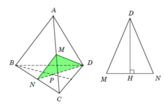
Trong tam giác BCD có: P là trọng tâm, N là trung điểm BC . Suy ra N , P , D thẳng hàng.
Vậy thiết diện là tam giác MND .
Xét tam giác MND , ta có ![]()
![]()
Do đó tam giác MND cân tại D .
Gọi H là trung điểm MN suy ra DH ⊥ MN
Diện tích tam giác ![]()
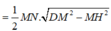
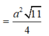

b: Ta có: BC=BH+HC
nên BC=4+9
hay BC=13cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{13}cm\\AC=3\sqrt{13}cm\end{matrix}\right.\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{ABC}=\dfrac{AC}{BC}=\dfrac{3\sqrt{13}}{13}\)
\(\cos\widehat{ABC}=\dfrac{AB}{BC}=\dfrac{2\sqrt{13}}{13}\)
\(\tan\widehat{ABC}=\dfrac{AC}{AB}=\dfrac{3}{2}\)
\(\cot\widehat{ABC}=\dfrac{AB}{AC}=\dfrac{2}{3}\)

b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{13}cm\\AC=3\sqrt{13}cm\end{matrix}\right.\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{ABC}=\dfrac{AC}{BC}=\dfrac{3\sqrt{13}}{13}\)
\(\cos\widehat{ABC}=\dfrac{AB}{BC}=\dfrac{2\sqrt{13}}{13}\)
\(\tan\widehat{ABC}=\dfrac{AC}{AB}=\dfrac{3}{2}\)
\(\cot\widehat{ABC}=\dfrac{AB}{AC}=\dfrac{2}{3}\)

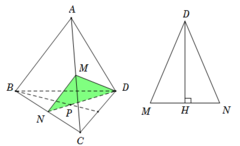
Trong tam giác BCD có: Plà trọng tâm, N là trung điểm BC .
Suy ra N; P; D thẳng hàng.
Vậy thiết diện là tam giác MND..
Xét tam giác MND, ta có M N = A B 2 = a ; D M = D N = A D 3 2 = a 3
Do đó tam giác MND cân tại D.
Gọi H là trung điểm MN suy ra DH và MN vuông góc với nhau..
Diện tích tam giác S Δ M N D = 1 2 M N . D H = 1 2 M N . D M 2 − M H 2 = a 2 11 4
Chọn C.