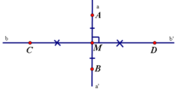
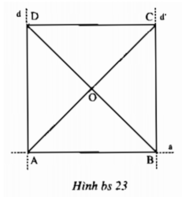
Cho hai đường thẳng d và d, vuông góc với nhau . Trên đường thẳng d lấy hai điểm A vafC . Trên đường thẳng d, lấy hai điểm B và D . Chứng minh rằng : ABbình+DCbình=ADbình+BCbình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

17 tháng 3 2020
Gọi giao điểm AC và BD là I
Pytago lần lượt vào các tam giác vuông AIB;BIC;CID;AID ta được :
\(AB^2=AI^2+BI^2\)
\(BC^2=BI^2+CI^2\)
\(CD^2=DI^2+CI^2\)
\(AD^2=DI^2+CI^2\)
\(\Rightarrow\hept{\begin{cases}AB^2+DC^2=AI^2+BI^2+CI^2+DI^2\\BC^2+AD^2=AI^2+BI^2+CI^2+DI^2\end{cases}}\)
\(\RightarrowĐPCM\)

CM
23 tháng 5 2018
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.