Cho góc xOy có số đo 120độ ,Điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc Ox (B thuộc Ox), kẻ AC vuông góc với Oy(C thuộc Oy). Tam giác ABC là tam giác gì? Vì sao ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 2 2022
Xét ΔABO vuông tại B và ΔACO vuông tại C có
OA chung
\(\widehat{BOA}=\widehat{COA}\)
Do đó: ΔABO=ΔACO
Suy ra: AB=AC
hay ΔABC cân tại A
mà \(\widehat{CAB}=180^0-120^0=60^0\)
nên ΔABC đều
15 tháng 1 2016
Bài này mình biết làm nhưng không biết vẽ hình trên máy tính
15 tháng 3 2016
Hai tam giác vuông ACO và ABO có:
=(gt)
AO chung
Nên suy ra ∆ACO=∆ABO(cạnh huyền góc nhọn)
Suy ra AC=AB.
Vây ∆ABC là tam giác cân(AB=AC).
29 tháng 1 2021
Ta có: OA là tia phân giác của \(\widehat{xOy}\)(gt)
nên \(\widehat{xOA}=\widehat{yOA}=\dfrac{\widehat{xOy}}{2}=\dfrac{120^0}{2}=60^0\)
hay \(\left\{{}\begin{matrix}\widehat{BOA}=60^0\\\widehat{COA}=60^0\end{matrix}\right.\)
Ta có: ΔAOC vuông tại C(AC\(\perp\)Oy tại C)
nên \(\widehat{CAO}+\widehat{COA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{CAO}=30^0\)
Ta có: ΔAOB vuông tại B(AB\(\perp Ox\) tại B)
nên \(\widehat{BAO}+\widehat{BOA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BAO}=30^0\)
Ta có: \(\widehat{CAB}=\widehat{CAO}+\widehat{BAO}\)(tia AO nằm giữa hai tia AB,AC)
\(\Leftrightarrow\widehat{CAB}=30^0+30^0\)
hay \(\widehat{CAB}=60^0\)
Xét ΔAOC vuông tại C và ΔAOB vuông tại B có
AO chung
\(\widehat{CAO}=\widehat{BAO}\left(=30^0\right)\)
Do đó: ΔAOC=ΔAOB(cạnh huyền-góc nhọn)
hay AC=AB(hai cạnh tương ứng)
Xét ΔABC có AB=AC(cmt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)(cmt)
nên ΔABC đều(Dấu hiệu nhận biết tam giác đều)
20 tháng 4 2017
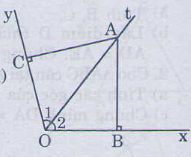
Hai tam giác vuông ACO và ABO có:
ˆO1O1^=ˆO2O2^(gt)
AO chung
Nên suy ra ∆ACO=∆ABO(cạnh huyền góc nhọn)
Suy ra AC=AB.
Vây ∆ABC là tam giác cân(AB=AC).
8 tháng 12 2016
Hình thím tự vẽ:
(tại cái bài lúc nãy đang làm gần xong cái tự nhiên "Ôi hỏng!!")
Gọi M là giao điểm của OA và BC
-Xét tam giác OAB và tam giác OAC có:
\(\widehat{AOB}\)=\(\widehat{AOC}\) (GT)
OA: cạnh chung
\(\widehat{B}\)=\(\widehat{C}\)=900 (GT)
=> tam giác OAB = tam giác OAC
(theo trường hợp cạnh huyền góc nhọn)
Ta có: OA là phân giác góc O
\(\widehat{AOB}\)=\(\widehat{AOC}\) = \(\frac{1}{2}\)\(\widehat{O}\) = \(\frac{1}{2}\)1200 = 600
Trong tam giác OAB có:
\(\widehat{O}\)+\(\widehat{A}\)+\(\widehat{B}\)=1800 (tổng 3 góc trong tam giác)
hay 600 + góc A + 900 = 1800
=> \(\widehat{A}\) = 300
Vì tam giác OAB = tam giác OAC
nên \(\widehat{OAB}\)=\(\widehat{OAC}\)=300
-Xét tam giác ABM và tam giác ACM có:
AM: cạnh chung
\(\widehat{BAM}\)=\(\widehat{CAM}\) (tam giác OAB = tam giác OAC)
AB = AC (tam giác OAB = tam giác OAC)
=> tam giác ABM = tam giác ACM (c.g.c)
=> \(\widehat{AMB}\)=\(\widehat{AMC}\) (2 góc tương ứng)
Mà \(\widehat{AMB}\)+\(\widehat{AMC}\) = 1800 (kề bù)
=> \(\widehat{AMB}\)=\(\widehat{AMC}\)=900
Trong tam giác ABM có:
\(\widehat{BAM}\)+\(\widehat{ABM}\)+\(\widehat{AMB}\)=1800 (tổng 3 góc của tam giác)
hay 300 + góc ABM + 900 = 1800
=> \(\widehat{ABM}\)=600
Vì tam giác ABM = tam giác ACM
nên \(\widehat{ABM}\)=\(\widehat{ACM}\)=600 (2 góc tương ứng)
Ta có: \(\widehat{BAM}\)+\(\widehat{CAM}\)=300+300=600
Trong tam giác ABC có:
\(\widehat{BAC}\)=\(\widehat{ABC}\)=\(\widehat{ACB}\)=600
=> tam giác ABC là tam giác đều
Vậy tam giác ABC là tam giác đều
"Sorry, hôm nay tớ bực bội wa"
8 tháng 12 2016
\(\Delta BOA\)vuông tại B có: BOA + OAB = 90o
\(\Delta COA\)vuông tại C có: COA + OAC = 90o
Mà BOA = COA vì OA là tia phân giác của BOC
=> OAB = OAC
Xét \(\Delta BOA\) và \(\Delta COA\) có:
BOA = COA (cmt)
OA là cạnh chung
BAO = CAO (cmt)
Do đó, \(\Delta BOA=\Delta COA\left(c.g.c\right)\)
=> AB = AC (2 cạnh tương ứng)
Như vậy tam giac ABC cân tại A
4 tháng 1 2016
Xét \(\Delta ABO\) và \(\Delta ACO\) có :
Góc ABO = Góc ACO ( = 90* )
AO là cạnh huyền chung của 2 tam giác
Góc AOB = Góc AOC ( OA là p/g góc xOy )
=> \(\Delta ABO=\Delta ACO\) ( cạnh huyền - góc nhọn )
=> AB=AC
Vì AB=AC => Tam giác ABC là tam giác cân .
Tick nha !
CM
12 tháng 12 2017
Hai tam giác vuông ABO (góc B = 90º) và ACO (góc C = 90º) có :
⇒ ΔABO = ΔACO (cạnh huyền – góc nhọn)
⇒ AB = AC (hai cạnh tương ứng) ⇒ ΔABC cân.
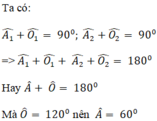
Tam giác cân ABC có góc A = 60º nên là tam giác đều.