P(x) = (3m-5n+1)x + (4m-n-10)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 10 2017
Đa thức P(x) bằng đa thức 0
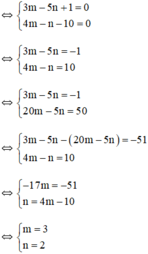
Vậy với m = 3 vào n = 2 thì đa thức P(x) bằng đa thức 0.
Kiến thức áp dụng
Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho và kết luận.
CM
24 tháng 11 2017
Đa thức P(x) bằng đa thức 0
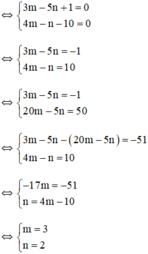
Vậy với m = 3 vào n = 2 thì đa thức P(x) bằng đa thức 0.
2 tháng 2 2019
Bài này là bài trong SGK có gì đâu -.-
Do một đa thức bằng đa thức 0 khi và chỉ khi tất cả các hệ số của nó bằng 0 nên P(x) = (3m – 5n + 1)x + (4m – n -10) = 0
\(\Leftrightarrow\hept{\begin{cases}3m-5n+1=0\\4m-n-10=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3m-5n=-1\\4m-n=10\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3m-5n=-1\\20m-5n=50\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}17m=51\\3m-5n=-1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=3\\n=2\end{cases}}\)
YN
7 tháng 2 2018
Để P(x) bằng đa thức 0 thì <=> \(\hept{\begin{cases}3m-5n+1=0\\4m-n-10=0\end{cases}}\)
(rồi giải bình thường thôi)
HY
7 tháng 2 2018
Để P(x) bằng đa thức 0 thì \(\hept{\begin{cases}3m-5n+1=0\\4m-n-10=0\end{cases}}\)
<=>\(\hept{\begin{cases}3m-5n=-1\\20m-5n=50\end{cases}}\)<=> \(\hept{\begin{cases}-17m=-51\\3m-5n=-1\end{cases}}\)
<=> \(\hept{\begin{cases}m=3\\9-5n=-1\end{cases}}\) <=> \(\hept{\begin{cases}m=3\\-5n=-10\end{cases}}\)
<=> \(\hept{\begin{cases}m=3\\n=2\end{cases}}\)
Vậy m=3, n=2 thì đa thức P(x) bằng đa thức 0
K
1
18 tháng 5 2020
a, Ta có m<n
⇔m+3 < n+3 (t/c)
b, Ta có m<n
⇔-3m>-3n(t/c)
c, Ta có m<n
⇔4m < 4n (t/c)
⇔4m-7 <4n-7 (t/c)
d, Ta có m<n
⇔-5m > -5n (t/c)
⇔-5m+10> -5n+10(t/c)
Hay 10-5m > 10-5n
chúc bạn học tốt !
4 tháng 4 2017
Ta có P(x) = (3m - 5n + 1)x + (4m - n -10)
Nếu P(x) = 0 ⇔ ⇔
⇔
⇔
⇔
⇔
HN
29 tháng 1 2021
Ta có P(x) = (3m - 5n + 1)x + (4m - n -10)
Nếu P(x) = 0 ⇔ ⇔
⇔
⇔
⇔
⇔
7 tháng 8 2020
\(\frac{4m-2n}{4m+5n}\) với \(\frac{m}{n}=\frac{1}{5}\)
Ta có : \(\frac{m}{n}=\frac{1}{5}\)hay \(\frac{m}{1}=\frac{n}{5}\)
Đặt \(\frac{m}{1}=\frac{n}{5}=k\Rightarrow\hept{\begin{cases}m=k\\n=5k\end{cases}}\)
Do đó \(\frac{4m-2n}{4m+5n}=\frac{4k-2\cdot5k}{4k+5\cdot5k}=\frac{4k-10k}{4k+25k}=\frac{-6k}{29k}=-\frac{6}{29}\)
b. \(\frac{2x+7}{3x-y}+\frac{2y-7}{3y-x}\)
Ta có : x - y = 7 => x = 7 + y
Do đó \(\frac{2x+7}{3x-y}+\frac{2y-7}{3y-x}=\frac{2\left(7+y\right)+7}{3\left(7+y\right)-y}+\frac{2y-7}{3y-\left(7+y\right)}\)
\(=\frac{14+2y+7}{21+3y-y}+\frac{2y-7}{3y-7-y}\)
\(=\frac{21+2y}{21+2y}+\frac{2y-7}{2y-7}=1+1=2\)
7 tháng 8 2020
a) \(\frac{m}{n}=\frac{1}{5}\Rightarrow\frac{m}{1}=\frac{n}{5}\)
Đặt \(\frac{m}{1}=\frac{n}{5}=k\Rightarrow\hept{\begin{cases}m=k\\n=5k\end{cases}}\)
Thế vào ta được :
\(\frac{4m-2n}{4m+5n}=\frac{4k-2.5k}{4k+5.5k}=\frac{4k-10k}{4k+25k}=\frac{-6k}{29k}=-\frac{6}{29}\)
b) x - y = 7 => x = 7 + y
Thế vào ta được :
\(\frac{2x+7}{3x-y}+\frac{2y-7}{3y-x}=\frac{2\left(7+y\right)+7}{3\left(7+y\right)-y}+\frac{2y-7}{3y-\left(7+y\right)}\)
\(=\frac{21+2y}{21+2y}+\frac{2y-7}{3y-7-y}\)
\(=\frac{21+2y}{21+2y}+\frac{2y-7}{2y-7}=1+1=2\)
LN
31 tháng 3 2019
1/Vì x,y,z là số chính phương nên x,y,z chia 3 dư 0 hoặc 1 và x,y,z chia 4 dư 0 hoặc 1 (tự CM)
TH1: x,y,z chia 3 dư 0 hoặc 1
Có: (x-y)(y-z)(z-x)
Vì x,y,z chia 3 dư 0 hoặc 1 nên có ít nhất 1 số chia hết cho 3
Suy ra: (x-y)(y-z)(z-x) chia hết cho 3 (1)
Tương tự: (x-y)(y-z)(z-x) chia hết cho 4 (2)
Từ (1) và (2)
Vậy (x-y)(y-z)(z-x) chia hết cho 12
2/ Có:
\(4m^2+m=5n^2+n\)
\(\Leftrightarrow5m^2-5n^2+m-n=m^2\)
\(\Leftrightarrow5\left(m-n\right)\left(m+n\right)+\left(m-n\right)=m^2\)
\(\Leftrightarrow\left(m-n\right)\left(5m+5n+1\right)=m^2\)
Do đó: để CM m-n và 5m+5n+1 là scp thì chúng phải là 2 số nguyên tố cùng nhau
Gọi d là \(ƯCLN\left(m-n;5m+5n+1\right)\)
Do đó: \(\hept{\begin{cases}m-n⋮d\\5m+5n+1⋮d\end{cases}\Leftrightarrow m^2⋮d^2}\Leftrightarrow m⋮d\)
Suy ra: \(n⋮d\)
Hay: \(5m+5n⋮d\)
Mà \(5m+5n+1⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
Vì thế m-n và 5m+5n+1 là 2 số nguyên tố cùng nhau
Vậy KL.....