tìm a biết đa thức \(fx=x^3-2x^2-5x+10+2a\)chia hết cho đa thức \(gx=x^2+x-2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)

a: 3x^3+2x^2-7x+a chia hêt cho 3x-1
=>3x^3-x^2+3x^2-x-6x+2+a-2 chia hết cho 3x-1
=>a-2=0
=>a=2
c: =>2x^2-6x+(a+6)x-3a-18+3a+19 chia x-3 dư 4
=>3a+19=4
=>3a=-15
=>a=-5
d: 2x^3-x^2+ax+b chiahêt cho x^2-1
=>2x^3-2x-x^2+1+(a+2)x+b-1 chia hết cho x^2-1
=>a+2=0 và b-1=0
=>a=-2 và b=1

=>2x^3-2x^2+7x^2-7x+5x-5+a+5 chia hết cho x-1
=>a+5=0
=>a=-5

a) A(x) = 5x4 - 5 + 6x3 + x4 - 5x - 12
= (5x4 + x4) + (- 5 - 12) + 6x3 - 5x
= 6x4 - 17 + 6x3 - 5x
= 6x4 + 6x3 - 5x - 17
B(x) = 8x4 + 2x3 - 2x4 + 4x3 - 5x - 15 - 2x2
= (8x4 - 2x4) + (2x3 + 4x3) - 5x - 15 - 2x2
= 4x4 + 6x3 - 5x - 15 - 2x2
= 4x4 + 6x3 - 2x2 - 5x - 15
b) C(x) = A(x) - B(x)
= 6x4 + 6x3 - 5x - 17 - (4x4 + 6x3 - 2x2 - 5x - 15)
= 6x4 + 6x3 - 5x - 17 - 4x4 - 6x3 + 2x2 + 5x + 15
= ( 6x4 - 4x4) + ( 6x3 - 6x3) + (- 5x + 5x) + (-17 + 15) + 2x2
= 2x4 - 2 + 2x2
= 2x4 + 2x2 - 2

a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
b) g(x) = x³ - 4x² + 5x - 1 = x³ - 3x² - x² + 3x + 2x - 6 + 5 = x²(x-3) - x(x-3) + 2(x-3) + 5
g(x) chia hết cho x-3 khi và chỉ khi 5 chia hết cho x-3 (5 là số nguyên tố nên chỉ xét các trường hợp)
TH1: x-3 = -5 <=> x = -2
TH2: x-3 = -1 <=> x = 2
TH3: x-3 = 1 <=> x = 4
TH4: x-3 = 5 <=> x = 8
Vậy có giá trị nguyên của x thỏa là {-1, 2, 4, 8}

Để : \(3x^3+2x^2-7x+a⋮3x-1\)<=> \(a-2=0\)
<=> \(a=2\)
Vậy a = 2
Để \(x^3+3x^2+5x+a⋮x+3\)<=> \(a-66=0\)
<=> \(a=66\)
Vậy a = 66

a: \(\Leftrightarrow2x^4-2x^3+2x^2+3x^3-3x^2+3x-2x^2+2x+2+a-2⋮x^2-x+1\)
=>a=2
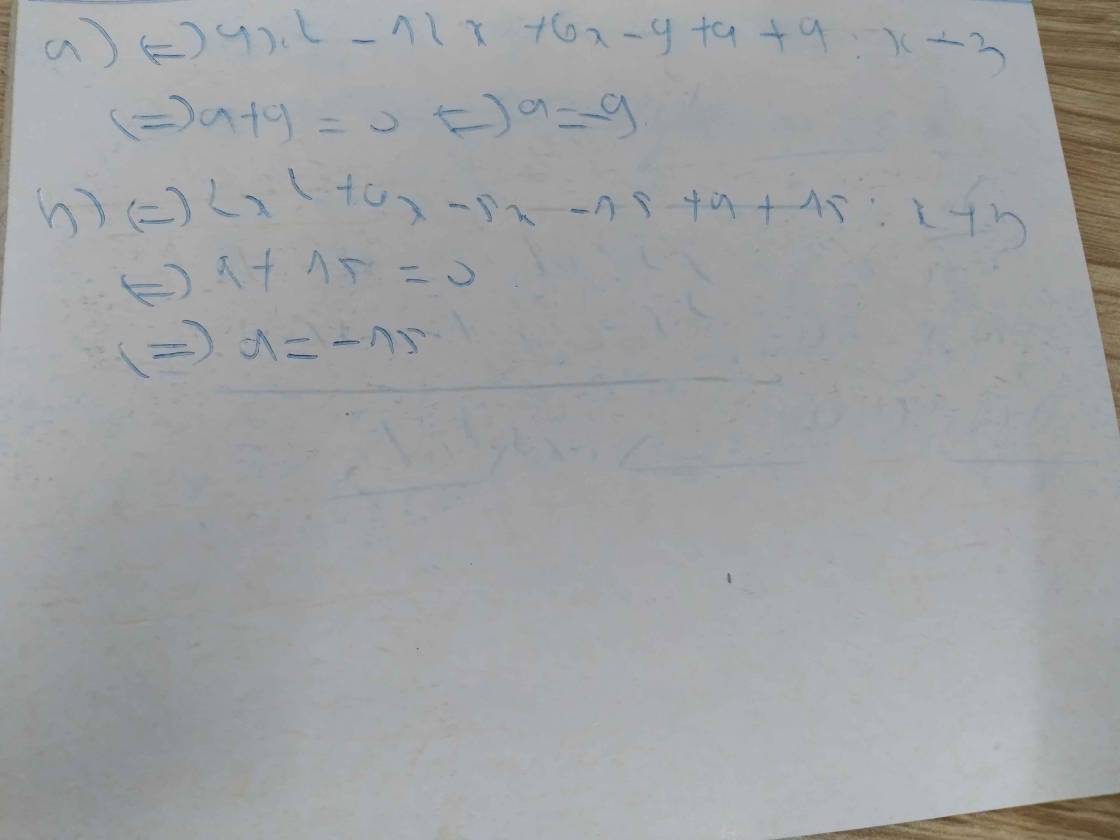
\(g\left(x\right)=x^2+x-2=x^2+2x-x-2\)
=> \(g\left(x\right)=x\left(x+2\right)-\left(x+2\right)=\left(x-1\right)\left(x+2\right)\)
Gọi thương của pháp chia là Q(x)
=> \(f\left(x\right)=g\left(x\right).Q\left(x\right)\)
=> \(x^3-2x^2-5x+10+2a=\left(x+2\right)\left(x-1\right).Q\left(x\right)\)
- Thay x = -2
=> \(\left(-2\right)^3-2.\left(-2\right)^2-5.\left(-2\right)+10+2a=\left(-2+2\right)\left(-2-1\right).Q\left(x\right)\)
=> \(4+2a=0\)
=> \(2a=-4\)
=> \(a=-2\)
- Thay x = 1
=> \(1^3-2.1^2-5.2+10+2a=\left(1+2\right)\left(1-1\right).Q\left(x\right)\)
=> \(1+2a=0\)
=> \(2a=-1\)
=> \(a=-0,5\)
KL: \(a\in\left\{-2;-0,5\right\}\)