Cho tam giác ABC cân tại A ( A ^ < 90 ° ) , kẻ đường phân giác AD. Trên tia đối của tia DC lấy điểm M sao cho MD = AD.
a.) Chứng minh tam giác DAM vuông cân tại D.
b) Kẻ BN vuông góc với AM tại N, các đường thẳng BN và AD cắt nhau tại O. Chứng minh O M ⊥ A B .
c) Chứng minh OB = OC.
d) Chứng minh AM // OC.
Cần lời giải chi tiết

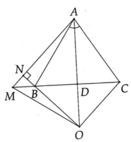

a) Xét ΔABD và ΔACD có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
Suy ra: \(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
hay \(\widehat{ADM}=90^0\)
Xét ΔADM có DA=DM(gt)
nên ΔADM cân tại D(Định nghĩa tam giác cân)
Xét ΔADM cân tại D có \(\widehat{ADM}=90^0\)(cmt)
nên ΔADM vuông cân tại D(Định nghĩa tam giác vuông cân)