Chứng minh rằng
-x2-2x-2<0 với mọi x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
22 tháng 7 2021
Lời giải:
a.
$A=(x+6)^2-(x+2)^2+2[(x-5)^2-(x-3)^2]$
$=(x+6-x-2)(x+6+x+2)+2[(x-5-x+3)(x-5+x-3)]$
$=4(2x+8)+2(-2)(2x-8)$
$=4(2x+8)-4(2x-8)=4[(2x+8)-(2x-8)]=4.16=64$ không phụ thuộc vào $x$
b.
$B=(x^3-2^3)-(x^3+2^3)=-16$ không phụ thuộc vào $x$
c.
$C=x^4+2x^2-[(x^2+3)^2-(2x)^2]$
$=x^4+2x^2-(x^4+6x^2-4x^2)$
$=x^4+2x^2-(x^4+2x^2)=0$ không phụ thuộc vào $x$
22 tháng 7 2021
a) Ta có: \(A=\left(x+6\right)^2+2\left(x-5\right)^2-\left(x+2\right)^2-2\left(x-3\right)^2\)
\(=x^2+12x+36+2\left(x^2-10x+25\right)-\left(x^2+4x+4\right)-2\left(x^2-6x+9\right)\)
\(=x^2+12x+36+2x^2-20x+50-x^2-4x-4-2x^2+12x-18\)
\(=34\)
b) Ta có: \(B=\left(x-2\right)\left(x^2+2x+4\right)-\left(x+2\right)\left(x^2-2x+4\right)\)
\(=x^3-8-x^3-8\)
=-16
c) Ta có: \(C=x^4+2x^2-\left(x^2-2x+3\right)\left(x^2+2x+3\right)\)
\(=x^4+2x^2-\left[\left(x^2+3\right)^2-4x^2\right]\)
\(=x^4+2x^2-\left(x^4+6x^2+9\right)+4x^2\)
\(=-9\)
Z
QA
5 tháng 2 2022
Trả lời:
a, \(x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTNN của biểu thức bằng 2 khi x = 3
b, \(-x^2+6x-11=-\left(x^2-6x+11\right)=-\left(x^2-6x+9+2\right)=-\left[\left(x-3\right)^2+2\right]\)
\(=-\left(x-3\right)^2-2\le-2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTLN của biểu thức bằng - 2 khi x = 3
c, \(x^2+2x+2=x^2+2x+1+1=\left(x+1\right)^2+1\ge1>0\forall x\inℤ\) (đpcm)
Dấu "=" xảy ra khi x + 1 = 0 <=> x = - 1
OY
21 tháng 10 2021
a) \(2x^2+2x+1=0\)
\(\Rightarrow2x^2+2x=-1\)
\(\Rightarrow2x\left(x+1\right)=-1\)
⇒ Pt vô nghiệm
21 tháng 10 2021
a: \(2x^2+2x+1=0\)
\(\text{Δ}=2^2-4\cdot2\cdot1=4-8=-4< 0\)
Vì Δ<0 nên phương trình vô nghiệm
PT
1
CM
17 tháng 6 2019
TXĐ: D = [0; 2]
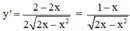
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 0 < x < 1.
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 < x < 2.
Vậy hàm số đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
T
10 tháng 10 2023
\(a)x^2-6x-2xy+12y\\=(x^2-2xy)-(6x-12y)\\=x(x-2y)-6(x-2y)\\=(x-2y)(x-6)\)
Bạn xem lại đề!
\(b\Big) (3-2x)(3+2x)+(2x+3)(2x-5)+4x\\=3^2-(2x)^2+(4x^2-10x+6x-15)+4x\\=9-4x^2+4x^2-10x+6x-15+4x\\=(9-15)+(-4x^2+4x^2)+(-10x+6x+4x)\\=-6\)
*Đã sửa đề*
\(c\Big) 4(x+1)^2+(2x-1)^2-8(x-1)(x+1)-4x\\=4(x^2+2x+1)+(2x)^2-2\cdot2x\cdot1x+1^2-8(x^2-1^2)-4x\\=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\\=(4x^2+4x^2-8x^2)+(8x-4x-4x)+(4+1+8)\\=13\)
*Đã sửa đề*
\(d\big) (3x+2)^2+(2x-7)^2-2(3x+2)(2x-7)-x^2+36x\\=[(3x+2)^2-2(3x+2)(2x-7)+(2x-7)^2]-x^2+36x\\=[(3x+2)-(2x-7)]^2-x^2+36x\\=(3x+2-2x+7)^2-x^2+36x\\=(x+9)^2-x^2+36x\\=(x+9-x)(x+9+x)+36x\\=9(2x+9)+36x\\=18x+81+36x\)
Bạn xem lại đề!
\(Toru\)
17 tháng 7 2021
a) Ta có: \(\dfrac{x^2+2x+1}{x^2+x}\)
\(=\dfrac{\left(x+1\right)^2}{x\left(x+1\right)}\)
\(=\dfrac{x+1}{x}\)
b) Ta có: \(\dfrac{x^2-4x+3}{x^2-x}\)
\(=\dfrac{\left(x-1\right)\left(x-3\right)}{x\left(x-1\right)}\)
\(=\dfrac{x-3}{x}\)
ta có.
-x²-2x-2=-(x²+2x+2) =-[(x²+2x+1)+1] =-(x+1)²-1
Do (x+1)²>=0 => -(x+1)²<0
=>-(x+1)²-1<0 hay -x²-2x-2<0 ( đpcm)