tim GTNN cua
a) A=x2 +3x 5/ x2+2x +1(x khac -1)
b) B = x4+x2+5/ x4+2x2+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`@` `\text {Ans}`
`\downarrow`

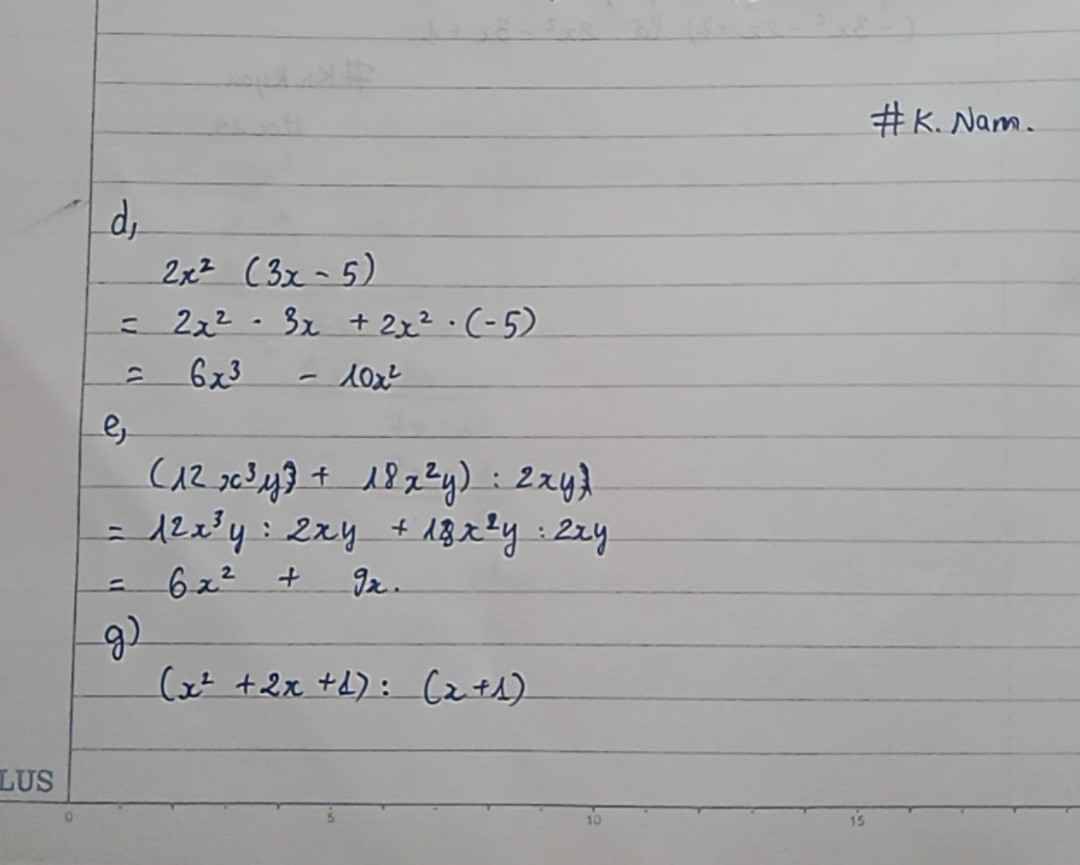

*Máy tớ cam hơi mờ, cậu thông cảm ._.*
Cậu viết lại rõ đề câu c, nhé.

\(a,=\left[x^2\left(x^2-x-1\right)+x^3+x^2-3x-1\right]:\left(x^2-x-1\right)\\ =\left[x^2\left(x^2-x-1\right)+x\left(x^2-x-1\right)+2x^2-2x-1\right]\\ =\left[x^2\left(x^2-x-1\right)+x\left(x^2-x-1\right)+2\left(x^2-x-1\right)+1\right]:\left(x^2-x-1\right)\\ =\left[\left(x^2+x+2\right)\left(x^2-x-1\right)+1\right]:\left(x^2-x-1\right)=x^2+x+2R1\)

c. Thay x = -1 vào A(x) và B(x) ta có:
A(-1) = 0, B(-1) = 2
Vậy x = -1 là nghiệm của A(x) nhưng không là nghiệm của B(x) (1 điểm)

b. Ta có:
A(x) + B(x) = x2 + 2x + 1 + x2 + 1 = 2x2 + 2x + 2 (0.5 điểm)
A(x) - B(x) = x2 + 2x + 1 - (x2 + 1) = 2x (0.5 điểm)

b: \(\dfrac{\left(x^2-1\right)\left(x^2+1\right)-2x\left(x^2-1\right)}{x^2-1}\)
\(=x^2-2x+1\)
\(=\left(x-1\right)^2\)
c: \(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
\(=5x^3+14x^2+12x+8\)

a.
$x^2-y^2-2x+2y=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)$
b.
$x^2(x-1)+16(1-x)=x^2(x-1)-16(x-1)=(x-1)(x^2-16)=(x-1)(x-4)(x+4)$
c.
$x^2+4x-y^2+4=(x^2+4x+4)-y^2=(x+2)^2-y^2=(x+2-y)(x+2+y)$
d.
$x^3-3x^2-3x+1=(x^3+1)-(3x^2+3x)=(x+1)(x^2-x+1)-3x(x+1)$
$=(x+1)(x^2-4x+1)$
e.
$x^4+4y^4=(x^2)^2+(2y^2)^2+2.x^2.2y^2-4x^2y^2$
$=(x^2+2y^2)^2-(2xy)^2=(x^2+2y^2-2xy)(x^2+2y^2+2xy)$
f.
$x^4-13x^2+36=(x^4-4x^2)-(9x^2-36)$
$=x^2(x^2-4)-9(x^2-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$
g.
$(x^2+x)^2+4x^2+4x-12=(x^2+x)^2+4(x^2+x)-12$
$=(x^2+x)^2-2(x^2+x)+6(x^2+x)-12$
$=(x^2+x)(x^2+x-2)+6(x^2+x-2)=(x^2+x-2)(x^2+x+6)$
$=[x(x-1)+2(x-1)](x^2+x+6)=(x-1)(x+2)(x^2+x+6)$
h.
$x^6+2x^5+x^4-2x^3-2x^2+1$
$=(x^6+2x^5+x^4)-(2x^3+2x^2)+1$
$=(x^3+x^2)^2-2(x^3+x^2)+1=(x^3+x^2-1)^2$

Dễ
Thế
Mà
Cũnhoir
Dc
Ạ
Chịu
Chắc
Phải
Ngu
Lamqs
Mới
Hỏi
Câu
Này

a: \(=\dfrac{3x^4-12x^3+12x^3-48x^2+47x^2-168x+168x-672+673}{x-4}\)
\(=3x^3+12x^2+47x+168+\dfrac{673}{x-4}\)
b: \(=\dfrac{x^4-3x^3-7x^2+3x^3-9x^2-21x+15x^2-45x-105+53x+91}{x^2-3x-7}\)
\(=x^2+3x+15+\dfrac{53x+91}{x^2-3x-7}\)
c: \(=\dfrac{x^3-3x^2-7x+x^2-3x-7}{x^2-3x-7}=x+1\)