Chiếc thang nhà Nam có 10 thanh ngang. Bạn hãy cho biết có bao nhiêu hình thang trong chiếc thang đó?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
K
1
AD
1 tháng 3 2021
Cứ mỗi cặp bậc thang (2 thang liền nhau) thì tạo thành một tứ giác
Nên 40 bậc thang thì tạo ra 39 bậc thang nhỏ
Số cặp cạnh cầu thang :
40x39:2=780(cặp)
=> Có 780 tứ giác trong hình thang đó.
#H
10 tháng 10 2018
Trên chiếc thang đó có số bậc thang là:
40 : 2 = 20 ( bậc thang)
Đáp số : 20 bậc thang
9 tháng 3 2021
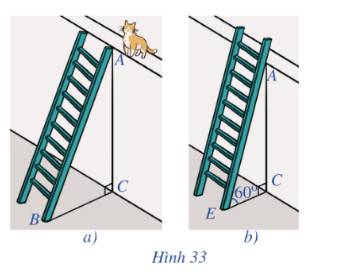
Gọi chiếc thang có cạnh AB, chân thang đến chân tường có cạnh BC, chân tường đến đầu chiếc thang là AC.
Xét ΔABC vuông tại C có:
CA2+CB2=AB2CA2+CB2=AB2 (Định lý Pi-ta-go)
CA2+52=132CA2+52=132
CA2=169−25CA2=169-25
CA2=144CA2=144
⇒ CA=12 m
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
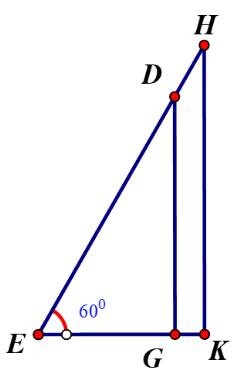
Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: \(EG = \frac{{DG}}{{\sqrt 3 }} = \frac{{x\sqrt 3 }}{3}\) (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(BC = \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} \)(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
\(\sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} - 0,5 = \frac{{x\sqrt 3 }}{3}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} = \frac{x}{{\sqrt 3 }} + 0,5\\ \Leftrightarrow \sqrt {2x + 1} = \frac{x}{{\sqrt 3 }} + 0,5\left( * \right)\end{array}\)
Ta có \(\frac{x}{{\sqrt 3 }} + 0,5 \ge 0 \Leftrightarrow \frac{x}{{\sqrt 3 }} \ge - \frac{1}{2}\)\( \Leftrightarrow x \ge - \frac{{\sqrt 3 }}{2}\) (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
\(\begin{array}{l}2x + 1 = {\left( {\frac{x}{{\sqrt 3 }} + 0,5} \right)^2}\\ \Leftrightarrow 2x + 1 = \frac{{{x^2}}}{3} + \frac{x}{{\sqrt 3 }} + 0,25\\ \Leftrightarrow \frac{{{x^2}}}{3} + \left( {\frac{{\sqrt 3 }}{3} - 2} \right)x - \frac{3}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x \approx 4,7\left( {tm} \right)\\x \approx - 0,5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy chiều cao của bức tường là 4,7 m.
Số hình thang là :
10 x 9: 2 =45 hình
Đáp số : 45 hình