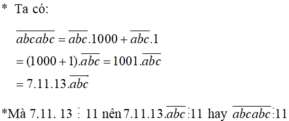1.Tính B=223223 × 328328 × 42154215 × 52245224 × 62356235 × 72487248 × 82638263 ×...
Đọc tiếp
1.Tính B=223223 × 328328 × 42154215 × 52245224 × 62356235 × 72487248 × 82638263 × 9280
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 10 2017
Đáp án cần chọn là: A
B = 2 2 3 ⋅ 3 2 8 ⋅ 4 2 15 ⋅ 5 2 24 ⋅ 6 2 35 ⋅ 7 2 48 ⋅ 8 2 63 ⋅ 9 2 80 = 2.2 1.3 ⋅ 3.3 2.4 ⋅ 4.4 3.5 ⋅ 5.5 4.6 ⋅ 6.6 5.7 ⋅ 7.7 6.8 ⋅ 8.8 7.9 ⋅ 9.9 8.10 = 2.3.4.5.6.7.8.9 1.2.3.4.5.6.7.8. ⋅ 2.3.4.5.6.7.8.9 3.4.5.6.7.8.9.10 = 9 1 ⋅ 2 10 = 9.2 1.10 = 9 5
29 tháng 11 2021
| x | 1 | 50 | -25 | \(\dfrac{5}{3}\) | -8 | 10 |
| y | 0,16 | 8 | -4 | 2\(\dfrac{2}{3}\) | -1,28 | 1,6 |
VT
1
21 tháng 10 2017
Có abcabc = abc . 1000 + abc
abcabc = abc . ( 1000 + 1 )
abcabc = abc . 1001
abcabc = abc . 11 . 91
Mà 11 \(⋮\)11 nên abc . 11 . 91 \(⋮\) 11
Vậy abcabc \(⋮\) 11 ( đpcm )
PT
1
PQ
5
16 tháng 8 2015
bạn có biết dấu hiệu chia hết cho 11 ko:hiệu của tổng các chữ số hàng chẵn(từ trái sang phải) vs tổng các chữ số hàng lẻ(từ trái sang phải) chia hết cho 11 thi số đó chia hết cho 11
bạn cứ thử đi và áp dụng vào bài toán
kiểu gì cũng ra
LN
21 tháng 10 2017
Theo bài ra ta có :
\(\overline{abcabc}\)
\(=\overline{abc}.1000+\overline{abc}.1\)
\(=\overline{abc}.\left(1000+1\right)\)
\(=\overline{abc}.1001\)
\(=\overline{abc}.11.91\)
\(=\left(\overline{abc}.91\right).11\)
\(\Rightarrow\overline{abcabc}⋮11\left(đpcm\right)\)
21 tháng 10 2017
Ta có:
\(\overline{abcabc}=1001\overline{abc}=11.91\overline{abc}\)
Vì \(11.91\overline{abc}\) \(⋮\) 11 nên \(\overline{abcabc}\) \(⋮\) 11
\(\Rightarrow\) ĐPCM(điều phải chứng minh)
DH
Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11 ( chẳng hạn số 328328 chia hết cho 11 )
3
4 tháng 10 2017
Ta có:
\(\overline{abcabc}=1001\overline{abc}=11.99\overline{abc}\)
Vì \(11.99\overline{abc}\) \(⋮\) 11 nên \(\overline{abcabc}\) \(⋮\) 11
\(\Rightarrow\text{Điều phải chứng minh}\)
4 tháng 10 2017
Vì x ⋮ 11 <=> (a0+a2+a4+...) - (a1+a3+a5+...) ⋮ 11
=> (c+a+b) - (b+c+a) = 0 ⋮ 11
Vậy dạng abcabc bao giờ cũng chia hết cho 11.
HD
4
D
11 tháng 11 2015
abc abc=abc.1000+abc=abc.(1000+1)
=abc.1001=abc.91.11
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11
vậy số abcabc lúc nào cũng chia hết cho 11