Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm có tọa độ x,y thỏa mãn điều kiện :
\(\left(x+2\right)^2+\left(y-3\right)^2=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 1 2022
Phương trình hoành độ giao điểm:
\(x^2=2\left(m-2\right)x+5\Leftrightarrow x^2-2\left(m-2\right)x-5=0\)
Do \(ac=-5< 0\Rightarrow\) phương trình luôn có 2 nghiệm trái dấu
\(\Rightarrow x_1< 0< x_2\Rightarrow x_2+2>0\)
Theo hệ thức Viet: \(x_1+x_2=2\left(m-2\right)\)
Ta có:
\(\left|x_1\right|-\left|x_2+2\right|=10\)
\(\Leftrightarrow-x_1-x_2-2=10\)
\(\Leftrightarrow-2\left(m-2\right)=12\)
\(\Leftrightarrow m=-4\)
AH
Akai Haruma
Giáo viên
5 tháng 7 2017
Giải:
Đặt \(z=a+bi\) với $a,b$ là các số thực
Ta có:
\(|z-3+4i|=2\Leftrightarrow |(a-3)+i(b+4)|=2\)
\(\Leftrightarrow (a-3)^2+(b+4)^2=4\)
Vậy tập hợp các điểm biểu diễn số phức $z$ nằm trên đường tròn tâm \((3;-4)\) bán kính \(R=2\)
11 tháng 7 2018
trên mặt phẳng tọa độ Oxy, tọa độ của điểm M(x; y) phải thỏa mãn điều kiện gì để hoành độ bằng 2?
Trả lời:
x=2
mk ko chắc lắm
CM
21 tháng 9 2019
Chọn D.
Gọi M(x; y) là điểm biểu diễn số phức z = x + yi, x, y ∈ R
Gọi A là điểm biểu diễn số phức 2
Gọi B là điểm biểu diễn số phức -2
Ta có: |z – 2| + |z + 2| = 10 ⇔ MB + MA = 10.
Ta có AB = 4.
Suy ra tập hợp điểm M biểu diễn số phức z là Elip với 2 tiêu điểm là A(2; 0), B( -2; 0) tiêu cự AB = 4 = 2c, độ dài trục lớn là 10 = 2a , độ dài trục bé là 
Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10 là elip có phương trình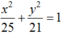 
18 tháng 1
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=2x-m+1\)
=>\(\dfrac{1}{2}x^2-2x+m-1=0\)
\(\Delta=\left(-2\right)^2-4\cdot\dfrac{1}{2}\left(m-1\right)\)
\(=4-2\left(m-1\right)=4-2m+2=-2m+6\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
=>-2m+6>0
=>-2m>-6
=>m<3
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{2}{\dfrac{1}{2}}=4\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{m-1}{\dfrac{1}{2}}=2\left(m-1\right)\end{matrix}\right.\)
\(x_1x_2\left(y_1+y_2\right)+48=0\)
=>\(\dfrac{1}{2}\left(x_1^2+x_2^2\right)\cdot x_1x_2+48=0\)
=>\(\dfrac{1}{2}\cdot2\cdot\left(m-1\right)\cdot\left[\left(x_1+x_2\right)^2-2x_1x_2\right]+48=0\)
=>\(\left(m-1\right)\cdot\left[4^2-2\cdot2\left(m-1\right)\right]+48=0\)
=>\(\left(m-1\right)\left(16-4m+4\right)+48=0\)
=>\(\left(m-1\right)\left(-4m+20\right)+48=0\)
=>\(\left(m-1\right)\left(-m+5\right)+12=0\)
=>\(-m^2+5m+m-5+12=0\)
=>\(-m^2+6m+7=0\)
=>\(m^2-6m-7=0\)
=>(m-7)(m+1)=0
=>\(\left[{}\begin{matrix}m=7\left(loại\right)\\m=-1\left(nhận\right)\end{matrix}\right.\)
12 tháng 9 2023
a)
- Với \(x = - 2 \Rightarrow f\left( { - 2} \right) = - 2;g\left( { - 2} \right) = - 2 + 3 = 1\);
- Với \(x = - 1 \Rightarrow f\left( { - 1} \right) = - 1;g\left( { - 1} \right) = - 1 + 3 = 2\);
- Với \(x = 0 \Rightarrow f\left( 0 \right) = 0;g\left( 0 \right) = 0 + 3 = 3\);
- Với \(x = 1 \Rightarrow f\left( 1 \right) = 1;g\left( 1 \right) = 1 + 3 = 4\);
- Với \(x = 2 \Rightarrow f\left( 2 \right) = 2;g\left( 2 \right) = 2 + 3 = 5\);
Ta có bảng sau:
\(x\) | –2 | –1 | 0 | 1 | 2 |
\(y = f\left( x \right) = x\) | –2 | –1 | 0 | 1 | 2 |
\(y = g\left( x \right) = x + 3\) | 1 | 2 | 3 | 4 | 5 |
b)
- Vẽ đồ thị hàm số \(y = f\left( x \right) = x\)
Cho \(x = 1 \Rightarrow y = f\left( x \right) = 1\). Ta vẽ điểm \(A\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).
- Các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) trong bảng trên là \(B\left( { - 2;1} \right);C\left( { - 1;2} \right);D\left( {0;3} \right);E\left( {1;4} \right);F\left( {2;5} \right)\).
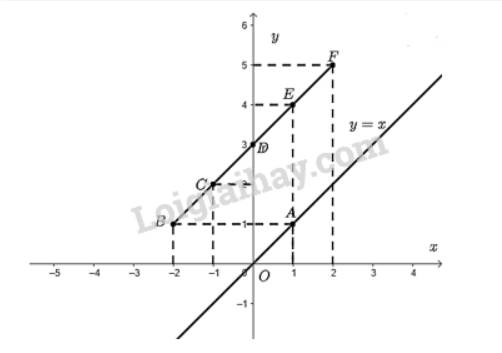
c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số \(y = g\left( x \right) = x = 3\) thẳng hàng với nhau.
Dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\):
Bước 1: Chọn hai điểm \(A;B\) phân biệt thuộc đồ thị hàm số \(y = g\left( x \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A;B\).
Đồ thị hàm số \(y = g\left( x \right)\) là đường thẳng đi qua hai điểm \(A;B\).
CM
11 tháng 9 2017
Chọn C.
Đặt 
;
suy ra 
Từ giả thiết, ta có:
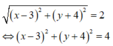
Tập hợp điểm biểu diễn các số phức z là đường tròn tâm I(3;-4) bán kính R=2.