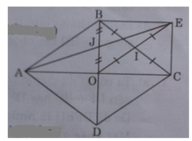
Cho hình thoi ABCD có O là giao điểm 2 đường chéo,I là trung điểm BC,E đối xứng với O qua I
a)Cm OCEB là hcn
b)Cm DOEC là hbh
c)F là giao điểm của AE và BC.Tính FB/FC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 3 2022
a: Xét tứ giác OCEB có
I là trung điểm của BC
I là trung điểm của OE
Do đó: OCEB là hình bình hành
mà \(\widehat{BOC}=90^0\)
nên OCEB là hình chữ nhật
b: Xét tứ giác DOEC có
DO//EC
DO=EC
Do đó: DOEC là hình bình hành
CM
18 tháng 10 2018
b)Ta có OA = OC (tính chất đường chéo hình thoi)
Mà OC = BE và OC // BE (cmt) nên OA = BE và OA // BE.
Do đó ABEO là hình bình hành
Ta có J là trung điểm của OB nên đường chéo thứ hai AI phải qua J và JA = JE.
⇒ E đối xứng với A qua trung điểm J của đoạn OB.
23 tháng 10 2021
a: Xét tứ giác AMCN có
O là trung điểm của AC
O là trung điểm của MN
Do đó: AMCN là hình bình hành
mình chẳng về được cái hình nữa
a, Xet tu giac OCEB co :
I la trung diem cua BC (IB=IC)
I là trung điểm của OE (IO=IE)
=> OCEB la hbh
Ma AC vuong voi BD
Hay AO vuong voi OB
=> goc O=90
Ma trong hinh binh hanh co 1 goc vuong la hinh chu nhat
=> OCEB la HCN
b, Xet tu giac DOEC co :
OB=OD
Ma : OB=CE (t/c HCN)
=> OD=CE
Va : OB//CE=>OD//CE
Vay ODCE là hình bình hành .
c, k pt