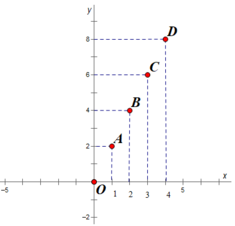
Cho các điểm biểu diễn các cặp giá trị tương ứng là: O(0;0); A(1;2); B(2;4); C(3;6); D(4;8)
Chứng minh rằng O;A;B;C;D thẳng hàng
Help me (Không cần vẽ hình cx đc)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 9 2018
Trên hình vẽ 0, A, B, C, D là vị trí của các điểm biểu diễn các cặp giá trị tương ứng của x và y trong câu a.
11 tháng 9 2023
a) Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2; - 6} \right);\left( { - 1; - 3} \right);\left( {0;0} \right);\left( {1;3} \right);\left( {2;6} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây
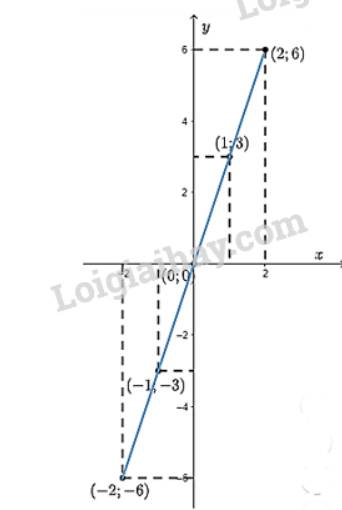
b) Các điểm vừa xác định được ở câu a đều nằm trên một đường thẳng.
18 tháng 12 2020
a) Thay x=1 vào hàm số y=2x-1, ta được:
\(y=2\cdot1-1=2-1=2\)
Thay x=-1 vào hàm số y=2x-1, ta được:
\(y=2\cdot\left(-1\right)-1=-2-1=-3\)
Thay x=0 vào hàm số y=2x-1, ta được:
\(y=2\cdot0-1=-1\)
Thay x=2 vào hàm số y=2x-1, ta được:
\(y=2\cdot2-1=4-1=3\)
Vậy: F(1)=2; F(-1)=-3; F(0)=-1; F(2)=3
b)
x 1 -1 0 2 y=2x-1 2 -3 -1 3
22 tháng 9 2023
a:
| x | 0,5 | 1 | 2 | 4 | 8 |
| \(y\) | -1 | 0 | 1 | 2 | 3 |
b:
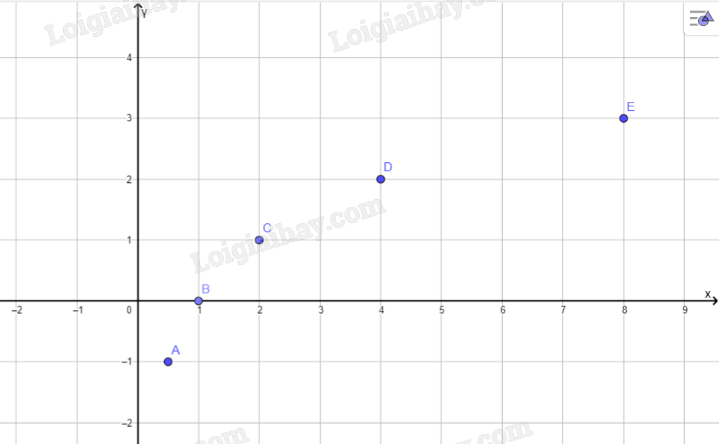
c: Tọa độ giao điểm của hàm số với trục hoành là B(2;0)
Đồ thị hàm số này ko cắt trục tung
d:
\(\lim\limits_{x\rightarrow0^+}log_2x=0\)
\(\lim\limits_{x\rightarrow+\infty}\left(log_2x\right)=+\infty\)
=>Hàm số này đồng biến trên TXĐ của nó là D=[0;+vô cực)
nay ban k có hàm số làm sao chứng minh dc