Cho tam giác ABC. Gọi M, N là các trung điểm tương ứng của AC, BC. Chứng minh rằng diện tích của hình thang ABMN bằng 3/4 diện tích của tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
16 tháng 3 2017
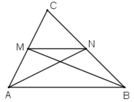
Vẽ hai trung tuyến AN, BM của ΔABC. Ta có:
N là trung điểm BC ⇒ 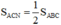 (chung chiều cao từ A, đáy CN = 1/2.BC)
(chung chiều cao từ A, đáy CN = 1/2.BC)
M là trung điểm CA ⇒ 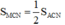 (chung chiều cao từ N, đáy CM = CA/2).
(chung chiều cao từ N, đáy CM = CA/2).
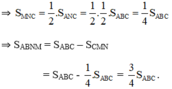

HL
28 tháng 6 2016
Ta có: N là tđ của BC
M là tđ của AC
=>MN là dtb của ΔABC => MN//AB
Kẻ đường cao CK của ΔABC (K ϵ AB) cắt MN tại H
Mà MN//AB nên: MN | CK
Như vậy hình thang ABMN có 2 cạnh đáy là MN ; AB và đường cao là HK
Ta lại có: N là trung điểm của BC
NH//BK (MN//AB)
............. hiccc làm dc nhiu đây thôi bận r
Gọi CK là đường cao của tam giác ABC
MI là đường cao của hình thang AMNB
MI là đường trung bình của tam giác ACK
Suy ra : MI=1/2 CK
S phần hình thang AMNB là :
((1/2+1)*1/2 )/2 =3/8
s tích phần tam giác ABC là :
(1*1)/2=1/2
S hình thang bằng số phần S tam giác là :
3/8 chia 1/2=3/2
Đ/S : 3/4 phần
Vẽ hai trung tuyến AN, BM của ΔABC. Ta có:
N là trung điểm BC \(\Rightarrow S_{ANC}=\frac{1}{2}S_{ABC}\)( chung chiều cao từ A , đáy \(CN=\frac{1}{2}BC\))
M là trung điểm CA \(\Rightarrow S_{MCN}=\frac{1}{2}S_{ACN}\)( chung chiều cao từ đáy N , đáy \(CM=\frac{CA}{2}\))
\(\Rightarrow S_{MNC}=\frac{1}{2}.S_{ANC}=\frac{1}{2}.\frac{1}{2}.S_{ANC}=\frac{1}{4}S_{ABC}\)
\(\Rightarrow S_{ABNM}=S_{ABC}-S_{CMN}\)
\(=S_{ABC}-\frac{1}{4}.S_{ABC}=\frac{3}{4}S_{ABC}\)