cho 2 điểm B(-1;-3); C(-1/3;1) điểm nào thuộc đồ thị hàm số trên ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Gọi \(D\left(a;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-9;3\right)\\\overrightarrow{AD}=\left(a-6;-3\right)\end{matrix}\right.\)
Do A; B; D thẳng hàng \(\Leftrightarrow\frac{a-6}{-9}=\frac{-3}{3}\Rightarrow a=15\) \(\Rightarrow D\left(15;0\right)\)
b/ \(\overrightarrow{AB}=\left(-1;5\right);\) \(\overrightarrow{AD}=\left(-2;10\right)\)
\(\Rightarrow\overrightarrow{AD}=2\overrightarrow{AB}\Rightarrow A,B,D\) thẳng hàng

\(\overrightarrow{AB}=\left(6;3\right)\) ; \(\overrightarrow{AC}=\left(5;-3\right)\)
Ta có \(\frac{5}{6}\ne\frac{-3}{3}\Rightarrow\overrightarrow{AB}\) và \(\overrightarrow{AC}\) ko cùng phương nên A;B;C ko thẳng hàng
\(\Rightarrow\) A;B;C là 3 đỉnh của 1 tam giác
2/ Gọi \(I\left(x;0\right)\Rightarrow\overrightarrow{AI}=\left(x+4;-1\right)\)
Để A;B;I thẳng hàng \(\Rightarrow\frac{x+4}{6}=-\frac{1}{3}\Rightarrow x+4=-2\Rightarrow x=-6\)
\(\Rightarrow I\left(-6;0\right)\)

Gọi (Q) và (R) theo thứ tự là mặt phẳng trung trực của AB và BC.
Những điểm cách đều ba điểm A, B, C là giao tuyến ∆ = (Q) ∩ (R).
(Q) đi qua trung điểm E(3/2; 1/2; 1) của AB và có n Q → = AB→ (1; -3; 0) do đó phương trình của (Q) là: x - 3/2 - 3(y - 1/2) = 0 hay x - 3y = 0
(R) đi qua trung điểm F(1; 1; 1) của BC và có n R → = BC → = (-2; 4; 0) do đó phương trình (R) là: x - 2y + 1 = 0
Ta có: n Q → ∧ n R → = (0; 0; -2).
Lấy D(-3; -1; 0) thuộc (Q) ∩ (R)
Suy ra ∆ là đường thẳng đi qua D và có vectơ chỉ phương u → (0; 0; 1)
nên có phương trình là: 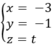

Lời giải:
PT hoành độ giao điểm:
\(x^3-2(m+1)x^2+(5m+1)x-2m-2=0\)
\(\Leftrightarrow (x-2)(x^2-2mx+m+1)=0\)
Vì \(A(2,0)\) nên hoành độ hai điểm \(B,C\) sẽ là nghiệm của PT \(x^2-2mx+m+1=0\)
Điều kiện: \(\Delta'=m^2-(m+1)>0\)
Khi đó, áp dụng định lý Viete, nếu $x_1,x_2$ là hai nghiệm của PT thì \(\left\{\begin{matrix} x_1+x_2=2m\\ x_1x_2=m+1\end{matrix}\right.\)
Nhận thấy hai điểm $B,C$ nằm trên $Ox$ mà một điểm nằm trong đường tròn \(x^2+y^2=1\) nên \((x_1-1)(x_2-1)<0\)
\(\Leftrightarrow x_1x_2-(x_1+x_2)+1<0\Leftrightarrow m+1-2m+1<0\)
\(\Leftrightarrow m>2\). Thử lại ta thấy thỏa mãn điều kiện \(\Delta'\)
Vậy \(m>2\)