cho đường thẳng m,n vuông góc với AB lần lượt tại A và B . Qua trung Diểm O của AB kẻ đoạn thẳng d cat71 m,n lần lượt tại C,D so sánh OC và OD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 6 2018
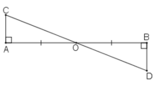
Xét ΔAOC và ΔBOD ta có:
∠(CAO) = ∠(DBO) = 90o
OA = OB (vì O là trung điểm của AB).
∠(AOC) = ∠(BOD) (hai góc đối đỉnh)
Suy ra: ΔAOC = ΔBOD (g.c.g)
Do đó, OC = OD (hai cạnh huyền tương ứng).
Vậy: OC = OD
TT
4 tháng 8 2020
câu a CHỨNG Minh AB = DC CHỨ sao AB = BC ĐC
A) XÉT \(\Delta ABC\)VÀ \(\Delta CDA\)CÓ
\(\widehat{ACB}=\widehat{CAD}\)( VÌ AD // BC , HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG )
AC LÀ CẠNH CHUNG
\(\widehat{BAC}=\widehat{DCA}\)( VÌ AB // DC , HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG )
=> \(\Delta ABC=\Delta CDA\left(g-c-g\right)\)
=> AD = BC (HAI CẠNH TƯƠNG ỨNG )
=> AB = DC ( HAI CẠNH TƯƠNG ỨNG )
TA CÓ M LÀ TRUNG ĐIỂM CỦA BC
\(\Rightarrow BM=CM=\frac{BC}{2}\left(1\right)\)
TA CÓ N LÀ TRUNG ĐIỂM CỦA AD
\(\Rightarrow AN=DN=\frac{AD}{2}\left(2\right)\)
TỪ (1) VÀ (2)
\(BM=CM=\frac{BC}{2}\)
\(AN=DN=\frac{AD}{2}\)
MÀ AD = BC ( CMT)
=> \(BM=CM=AN=DN\)
XÉT \(\Delta BAM\)VÀ \(\Delta DCN\)CÓ
\(BA=DC\)(VÌ \(\Delta ABC=\Delta CDA\))
\(\widehat{ABM}=\widehat{CDN}\)(VÌ \(\Delta ABC=\Delta CDA\))
\(BM=DN\left(cmt\right)\)
=>\(\Delta BAM=\Delta DCN\left(c-g-c\right)\)
=> AM = CN (HAI CẠNH TƯƠNG ỨNG )
c) XÉT TỨ GIÁC ABCD
ta có \(AD=BC\left(cmt\right);AB=CD\left(cmt\right)\)
=> TỨ GIÁC ABCD LÀ HÌNH THOI
=> CÁC ĐƯỜNG CHÉO CẮT NHAU TẠI TRUNG ĐIỂM CỦA NÓ
=> \(OA=OC;OB=OD\)
5 tháng 8 2020
mượn hình của Lê Trí Tiên làm tiếp câu (d)
vì M là trung điểm AD và O là trung điểm của AC => ON là đường trung bình tam giác ACD
=> ON //DC (1)
chứng minh tương tự ta có: OM là đường trung bình tam giác ACB
=> OM // AB mà AB // CD => OM // DC (2)
từ (1) (2) => M,O,N thằng hàng (đpcm)
5 tháng 8 2020
Bạn tự vẽ hình nhé
a, Xét \(\Delta ABC\)và \(\Delta CDA\), ta có
\(\widehat{DAC}=\widehat{ACB}\left(gt\right)\)
AC: cạnh chung
\(\widehat{BAC}=\widehat{DCA}\left(gt\right)\)
do đó: \(\Delta ABC=\Delta CDA\left(g.c.g\right)\)
=>AD=BC(2 cạnh tương ứng)
=>AB=DC(2 cạnh tương ứng)
b, Ta có: BC=AD(CMT)
=>\(\frac{1}{2}BC=\frac{1}{2}AD\)=>MC=AN
Xét \(\Delta MAC\)và \(\Delta NCA\), ta có:
MC=AN(CMT)
\(\widehat{NAC}=\widehat{MCA}\) (2 góc so le trong)
AC:cạnh chung
do đó: \(\Delta MAC=\Delta NCA\left(c.g.c\right)\)
=>AM=CN(2 cạnh tương ứng)
c, Xét \(\Delta OAD\)và \(\Delta OCB\), ta có:
\(\widehat{DAO}=\widehat{BCO}\)(2 góc so le trong)
BC=AD(CMT)
\(\widehat{OBC}=\widehat{ADO}\)(2 góc so le trong)
do đó \(\Delta AOD=\Delta COB\left(g.c.g\right)\)
=> OA=OC(2 cạnh tương ứng)
=>OB=OD(2 cạnh tương ứng)
d,Sử dụng tiên đề Ơ-Clit...Bạn suy nghĩ đi mk chưa có cách giải chi tiết
Chúc bạn học tốt