cho đa thứcE=x3-4x2+7x+a-6
xác định a để đa thức E chia hết cho đa thức x-2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có

Vì phần dư R = 0 nên Phép chia đa thức (2 x 3 – 26x – 24) cho đa thức x 2 + 4x + 3 là phép chia hết.
Do đó (I) đúng.
Lại có
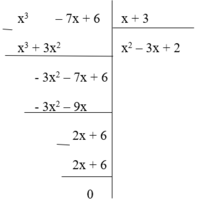
Nhận thấy phần dư R = 0 nên phép chia đa thức ( x 3 – 7x + 6) cho đa thức x + 3 là phép chia hết. Do đó (II) đúng
Đáp án cần chọn là: A

b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)

a: \(\Leftrightarrow2x^4-2x^3+2x^2+3x^3-3x^2+3x-2x^2+2x+2+a-2⋮x^2-x+1\)
=>a=2

a: =>2x^3-4x^2-3x^2+6x+4x-8+a+8 chia hết cho x-2
=>a+8=0
=>a=-8
b: =>2x^3+x^2-x^2-0,5x-0,5x+0,25+m-0,25 chia hết cho 2x+1
=>m-0,25=0
=>m=0,25

a: \(\dfrac{A}{B}=\dfrac{x^3+x^2+2x^2+2x+x+1-3}{x+1}=x^2+2x+1-\dfrac{3}{x+1}\)
b: Để A chia hết cho B thì \(x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-2;2;-4\right\}\)
Để E chia hết cho x-2<=> Tồn tại một đa thức gx sao cho E=gx. (x-2)
=>x3-4x2+7x+a-6=gx.(x-2) với mọi x (1)
Thay x=2 vào (1) ta được
23-4.22+7.2+a-6=0
<=>8-16+14-6+a=0
<=>a=0