Giả sử x=a/m;y=b/m(a,b,m thuộc Z,m>0) và x<y.Chứng tỏ rằng:
Nếu z=a+b/2m thì ta có x<z<y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NQ
1

Những câu hỏi liên quan

TN
14 tháng 8 2017
Giả sử x = a/m, y = b/m (a, b, m ∈ Z, b # 0) và x < y. Hãy chứng tỏ rằng nếu chọn z = (a + b)/2m thì ta có x < z < y.

BY
0

BN
0


CM
16 tháng 7 2019
Vì x < y nên 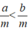 mà m > 0 nên a < b. Ta có
mà m > 0 nên a < b. Ta có
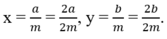
Chọn số 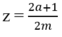 . Do 2a < 2a + 1 và m > 0 nên
. Do 2a < 2a + 1 và m > 0 nên 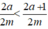 hay x < z. (1)
hay x < z. (1)
Do a < b và a; b ∈ Z nên a + 1 ≤ b suy ra 2a + 2 ≤ 2b.
Ta có 2a + 1 < 2a + 2 ≤ 2b nên 2a + 1 < 2b, do đó 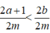 hay z < y. (2)
hay z < y. (2)
Từ (1) và (2) suy ra: x < z < y
VH
0

NA
0

PM
1

AH
Akai Haruma
Giáo viên
26 tháng 6 2021
Lời giải:
Áp dụng BĐT Cô - si:
\(P=ax^m+\frac{b}{x^n}=\frac{a}{n}x^m+\frac{a}{n}x^m+...+\frac{a}{n}x^m+\frac{b}{mx^n}+...+\frac{b}{mx^n}\)
\(=(m+n)\sqrt[m+n]{(\frac{a}{n})^n.x^{mn}.(\frac{b}{m})^m.\frac{1}{x^{mn}}}\)
\(=(m+n)\sqrt[m+n]{\frac{a^nb^m}{n^n.m^m}}\)
T
0

\(\frac{a}{m}<\frac{b}{m}\Rightarrow a\)<b
\(\Rightarrow x=\frac{2a}{2m};y=\frac{2b}{2m}\)
2a<a+b<2b \(\Rightarrow x=\frac{2a}{2m}\)<\(z=\frac{a+b}{2m}\)<\(y=\frac{2b}{2m}\)
=>đpcm