Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB=a, AD=a căn2, SA=a và SA vuông góc với mp đáy. Gọi M là trung điểm của AD và I là giao của BM và AC. Chứng minh (SAC) vuông góc (SMB)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 11 2019
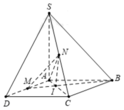
Đáp án A
Vì A M / / B C ⇒ I M I B = M A B C = 1 2 ⇒ d I ; A D d B ; A D = 1 3
|
Suy ra S Δ I M A = 1 2 d I ; A D . A M = 1 2 . 1 3 d B ; A D . 1 2 A D = S A B C D 12
Mà N là trung điểm của S C ⇒ d N ; A B C D = 1 2 d S ; A B C D
Vậy V A M N I V S . A B C D = d N ; A B C D d S ; A B C D . S Δ I M A S A B C D = 1 2 . 1 12 = 1 24
CM
25 tháng 11 2018
Đáp án là D
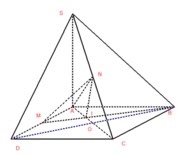
Coi hình chóp AMNI với điểm N làm đỉnh và AMI làm đáy
+) Từ N là trung điểm của SC nên đường cao
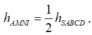
+) Lấy O là tâm hình chữ nhật ta có BM, AO là các trung tuyến nên I là trọng tâm tam giác ABD nên
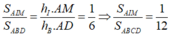
+) Suy ra
15 tháng 6 2023
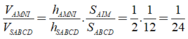
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
Ta có: \(AC=\sqrt{AB^2+BC^2}=a\sqrt{3}\) ;
\(AM=\dfrac{AD}{2}=\dfrac{a\sqrt{2}}{2}\Rightarrow BM=\sqrt{AB^2+AM^2}=\dfrac{a\sqrt{6}}{2}\)
Áp dụng định lý talet:
\(\dfrac{AI}{IC}=\dfrac{MI}{BI}=\dfrac{AM}{BC}=\dfrac{1}{2}\Rightarrow\left\{{}\begin{matrix}IC=\dfrac{2}{3}AC=\dfrac{2a\sqrt{3}}{3}\\IB=\dfrac{2}{3}BM=\dfrac{a\sqrt{6}}{3}\end{matrix}\right.\)
\(\Rightarrow IB^2+IC^2=2a^2=BC^2\)
\(\Rightarrow\Delta IBC\) vuông tại I \(\Rightarrow BM\perp AC\Rightarrow BM\perp\left(SAC\right)\)
Mà \(BM\in\left(SMB\right)\Rightarrow\left(SAC\right)\perp\left(SMB\right)\)