Cho hàm số \(y=x+1+\dfrac{1}{x-1}\) (C) . Tìm các điểm A thuộc đồ thị (C) sao cho tiếp tuyến tại A cắt trục hoành, trục tung theo thứ tự M,N (M,N khác O) sao cho ON=2OM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y=\left(2m-1\right)x+m+1\left(m\ne\dfrac{1}{2}\right)\)
\(x=0\Rightarrow y=m+1\Rightarrow A\left(0;m+1\right)\Rightarrow OA=\left|m+1\right|\)
\(y=0\Rightarrow x=\dfrac{-m-1}{2m-1}=\dfrac{m+1}{1-2m}\Rightarrow B\left(\dfrac{m+1}{1-2m};0\right)\Rightarrow OB=\left|\dfrac{m+1}{1-2m}\right|\)
\(\Delta OAB-cân-tạiO\Leftrightarrow OA=OB>0\Rightarrow\left\{{}\begin{matrix}\left|m+1\right|>0\\\left|\dfrac{m+1}{1-2m}\right|>0\end{matrix}\right.\)\(\Leftrightarrow-1< m< \dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}m+1=\dfrac{m+1}{1-2m}\\m+1=\dfrac{-\left(m+1\right)}{1-2m}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m=-1\left(ktm\right);m=0\left(tm\right)\\m=1\left(tm\right);m=-1\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)
PT giao Ox và Oy:
\(\left\{{}\begin{matrix}y=0\Rightarrow\left(2m-1\right)x=-\left(m+1\right)\Rightarrow x=\dfrac{m+1}{1-2m}\Rightarrow A\left(\dfrac{m+1}{1-2m};0\right)\Rightarrow OA=\left|\dfrac{m+1}{1-2m}\right|\\x=0\Rightarrow y=m+1\Rightarrow B\left(0;m+1\right)\Rightarrow OB=\left|m+1\right|\end{matrix}\right.\)
\(\Delta AOB\text{ cân}\\ \Leftrightarrow OA=OB\Leftrightarrow\left|\dfrac{m+1}{1-2m}\right|=\left|m+1\right|\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{m+1}{1-2m}=m+1\\\dfrac{m+1}{2m-1}=m+1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left(m+1\right)\left(1-2m\right)-\left(m+1\right)=0\\\left(m+1\right)\left(2m-1\right)-\left(m+1\right)=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}-2m\left(m+1\right)=0\\\left(m+1\right)\left(2m-2\right)=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=1\\m=-1\end{matrix}\right.\)

Gọi k là hệ số góc của tiếp tuyến tại M, N thì \(x_M;x_N\) là nghiệm của phương trình :
\(f'\left(x\right)=k\Leftrightarrow3x^2-6x-k=0\)
Để tồn tại hai tiếp điểm M, N thì phải có \(\Delta'>0\Leftrightarrow k>-3\)
Ta có \(y=f'\left(x\right)\left(\frac{1}{3}x-\frac{1}{3}\right)-2x+2\)
Từ \(f'\left(x_M\right)=f'\left(x_N\right)=k\) suy ra phương trình đường thẳng MN là :
\(y=\left(\frac{k}{3}-2\right)x+2-\frac{k}{3}\), khi đó \(A\left(1;0\right);B\left(0;\frac{6-k}{3}\right)\)
Ta có \(AB^2=10\Leftrightarrow k=15\) (do k > -3)
Từ đó ta có 2 tiếp tuyến cần tìm là :
\(y=15x-12\sqrt{6}-15\)
\(y=15x+12\sqrt{6}-15\)

a) Để đồ thị hàm số đi qua điểm A(-2;3), ta thay x = -2 và y = 3 vào phương trình hàm số:
3 = (2m+1)(-2) + 3m - 1
Giải phương trình, ta có:
3 = -4m - 2 + 3m - 1
3 = -m - 3
m = -6
b) Để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2, ta thay x = 2 vào phương trình hàm số:
0 = (2m+1)(2) + 3m - 1
Giải phương trình, ta có:
0 = 4m + 2 + 3m - 1
0 = 7m + 1
m = -1/7
c) Để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2, ta thay y = 2 vào phương trình hàm số:
2 = (2m+1)x + 3m - 1
2 = (2m+1)x + 3m - 1
(2m+1)x + 3m = 3
d) Để đồ thị hàm số cắt đường thẳng Y = x + 2 tại điểm có hoành độ bằng 3, ta thay x = 3 vào phương trình hàm số và đường thẳng:
(2m+1)(3) + 3m - 1 = 3 + 2
Giải phương trình, ta có:
6m + 4 = 5
m = 1/6
e) Để đồ thị hàm số cắt đường thẳng Y = -x - 3 tại điểm có tung độ bằng -1, ta thay y = -1 vào phương trình hàm số và đường thẳng:
-1 = (2m+1)x + 3m - 1 = -x - 3
(2m+1)x + 3m = -2
g) Để vẽ đồ thị hàm số khi m = 2, ta thay m = 2 vào phương trình hàm số:
Y = (2(2)+1)x + 3(2) - 1
Y = 5x + 5
a: Thay x=-2 và y=3 vào (d), ta được:
-2(2m+1)+3m-1=3
=>-4m-2+3m-1=3
=>-m-3=3
=>m+3=-3
=>m=-6
b: Thay x=2 và y=0 vào (d), ta được:
2(2m+1)+3m-1=0
=>7m+3=0
=>m=-3/7
c: Thay x=0 và y=2 vào (d), ta được:
0(2m+1)+3m-1=2
=>3m-1=2
=>m=1
d: Thay x=3 vào y=x+2, ta được:
y=3+2=5
Thay x=3; y=5 vào (d), ta được:
3(2m+1)+3m-1=5
=>9m+2=5
=>9m=3
=>m=1/3
e: Thay y=-1 vào y=-x-3, ta được:
-x-3=-1
=>x+3=1
=>x=-2
Thay x=-2 và y=-1 vào (d), ta được:
-2(2m+1)+3m-1=-1
=>-4m-2+3m-1=-1
=>-m-3=-1
=>-m=2
=>m=-2
g: Khi m=2 thì (d) sẽ là:
y=(2*2+1)x+3*2-1
=5x+5

a. Để đồ thị qua A
\(\Rightarrow-1=-3m+m-1\)
\(\Leftrightarrow m=0\)
b. Để đồ thị cắt trục tung tại điểm có tung độ 2
\(\Rightarrow m-1=2\)
\(\Leftrightarrow m=3\)
c. Để đồ thị cắt trục hoành tại điểm có hoành độ 3
\(\Rightarrow0=3m+m-1\)
\(\Leftrightarrow m=\dfrac{1}{4}\)

a: Thay x=2 và y=0 vào y=(m+1)x-1, ta được:
2(m+1)-1=0
=>2(m+1)=1
=>m+1=1/2
=>\(m=\dfrac{1}{2}-1=-\dfrac{1}{2}\)
b: Thay x=0 và y=2 vào y=(m+1)x-1, ta được:
\(0\cdot\left(m+1\right)-1=2\)
=>-1=2(vô lý)

a)Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
\(\Rightarrow2=\left(m-2\right).0+m\) \(\Leftrightarrow m=2\)
Vậy m=2 thì đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3
\(\Rightarrow0=\left(m-2\right)\left(-3\right)+m\) \(\Leftrightarrow m=3\)
Vậy...
c) Hàm số đi qua điểm A(1;2)
\(\Rightarrow2=\left(m-2\right).1+m\)\(\Leftrightarrow m=2\)
Vậy...
a) Đồ thị cắt trục tung tại điểm có tung độ bằng 2
\(\Rightarrow\) điểm đó có tọa độ là \(\left(0;2\right)\)
\(\Rightarrow2=m\)
b) Đồ thị cắt trục hoành tại điểm có hoành độ bằng -3
\(\Rightarrow\) điểm đó có tọa độ là \(\left(-3;0\right)\)
\(\Rightarrow0=-3m+6+m=-2m+6\Rightarrow m=3\)
c) Đồ thị đi qua điểm \(A\left(1;2\right)\)
\(\Rightarrow2=m-2+m\Rightarrow m=2\)

a: Thay x=-1 và y=2 vào (d), ta được:
\(-\left(m-2\right)+n=2\)
=>-m+2+n=2
=>-m+n=0
=>m-n=0(1)
Thay x=3 và y=-4 vào (d), ta được:
\(3\left(m-2\right)+n=-4\)
=>3m-6+n=-4
=>3m+n=2(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}m-n=0\\3m+n=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m-n+3m+n=2\\m-n=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m=2\\n=m\end{matrix}\right.\Leftrightarrow n=m=\dfrac{1}{2}\)
b: Thay x=0 và \(y=1-\sqrt{2}\) vào (d), ta được:
\(0\left(m-2\right)+n=1-\sqrt{2}\)
=>\(n=1-\sqrt{2}\)
Vậy: (d): \(y=\left(m-2\right)x+1-\sqrt{2}\)
Thay \(x=2+\sqrt{2}\) và y=0 vào (d), ta được:
\(\left(m-2\right)\cdot\left(2+\sqrt{2}\right)+1-\sqrt{2}=0\)
=>\(\left(m-2\right)\left(2+\sqrt{2}\right)=\sqrt{2}-1\)
=>\(m-2=\dfrac{\sqrt{2}-1}{2+\sqrt{2}}=\dfrac{-4+3\sqrt{2}}{2}\)
=>\(m=\dfrac{-4+3\sqrt{2}+4}{2}=\dfrac{3\sqrt{2}}{2}\)
c: 2y+x-3=0
=>2y=-x+3
=>\(y=-\dfrac{1}{2}x+\dfrac{3}{2}\)
Để (d) vuông góc với đường thẳng y=-1/2x+3/2 thì
\(-\dfrac{1}{2}\left(m-2\right)=-1\)
=>m-2=2
=>m=4
Vậy: (d): \(y=\left(4-2\right)x+n=2x+n\)
Thay x=1 và y=3 vào y=2x+n, ta được:
\(n+2\cdot1=3\)
=>n+2=3
=>n=1
d: 3x+2y=1
=>\(2y=-3x+1\)
=>\(y=-\dfrac{3}{2}x+\dfrac{1}{2}\)
Để (d) song song với đường thẳng \(y=-\dfrac{3}{2}x+\dfrac{1}{2}\) thì
\(\left\{{}\begin{matrix}m-2=-\dfrac{3}{2}\\n\ne\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=\dfrac{1}{2}\\n\ne\dfrac{1}{2}\end{matrix}\right.\)
Vậy: (d): \(y=\left(\dfrac{1}{2}-2\right)x+n=-\dfrac{3}{2}x+n\)
Thay x=1 và y=2 vào (d), ta được:
\(n-\dfrac{3}{2}=2\)
=>\(n=2+\dfrac{3}{2}=\dfrac{7}{2}\left(nhận\right)\)
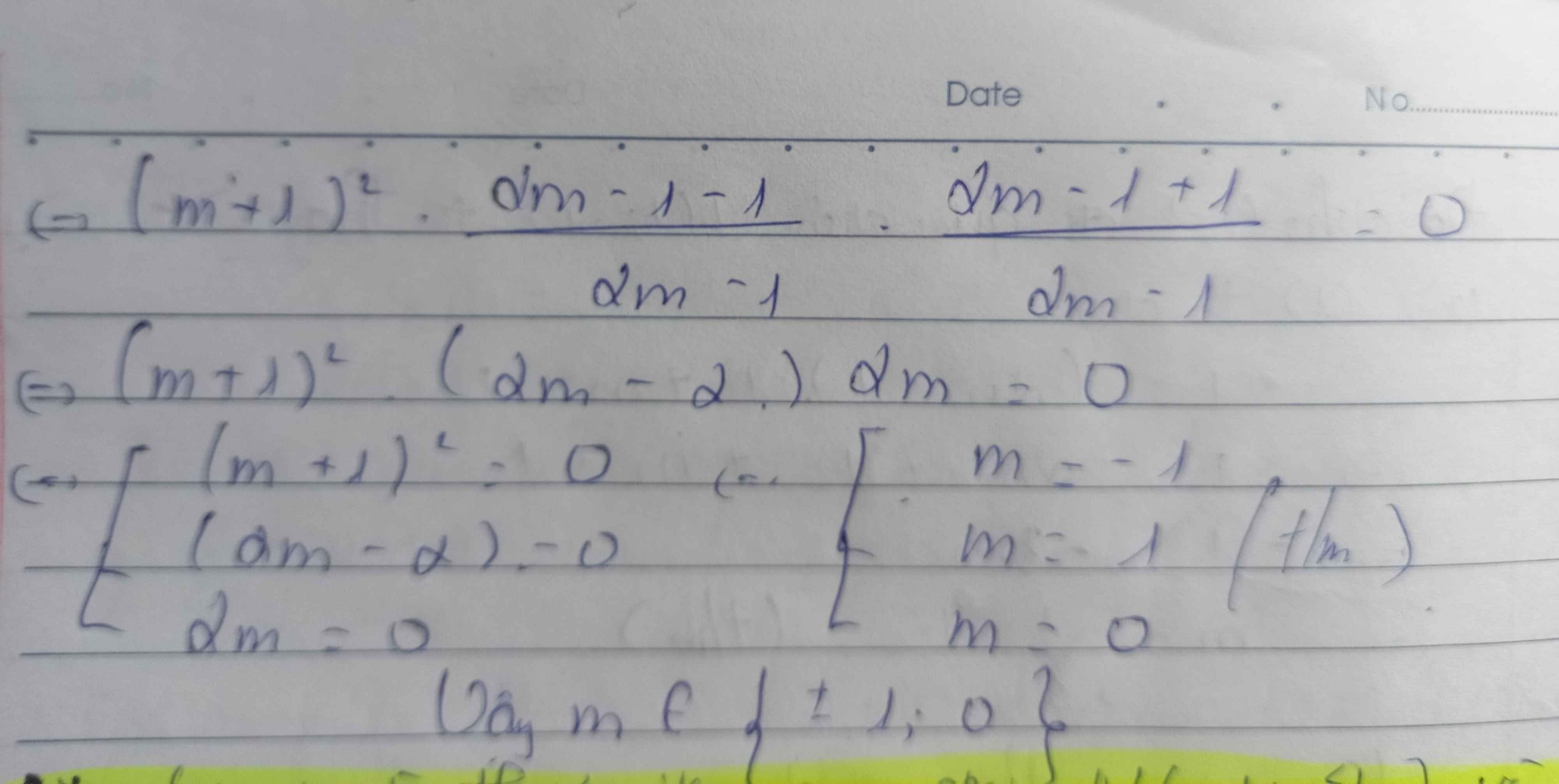

\(y'=1-\dfrac{1}{\left(x-1\right)^2}\)
Tiếp tuyến d tại \(A\left(a;a+1+\dfrac{1}{a-1}\right)\) có dạng:
\(y=\left(1-\dfrac{1}{\left(a-1\right)^2}\right)\left(x-a\right)+a+1+\dfrac{1}{a-1}\)
\(\Leftrightarrow y=\dfrac{a^2-2a}{\left(a-1\right)^2}x+\dfrac{a^2}{\left(a-1\right)^2}\)
\(\Rightarrow M\left(\dfrac{a^2}{2a-a^2};0\right)\) ; \(N\left(0;\dfrac{a^2}{\left(a-1\right)^2}\right)\Rightarrow\left\{{}\begin{matrix}OM=\dfrac{a^2}{\left|2a-a^2\right|}\\ON=\dfrac{a^2}{\left(a-1\right)^2}\end{matrix}\right.\)
\(\dfrac{a^2}{\left(a-1\right)^2}=\dfrac{2a^2}{\left|2a-a^2\right|}\Leftrightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\\left|a^2-2a\right|=2\left(a^2-2a+1\right)\end{matrix}\right.\)
Đặt \(a^2-2a=t\Rightarrow\left|t\right|=2\left(t+1\right)\) (với \(t\ge-1\))
\(\Leftrightarrow\left[{}\begin{matrix}2t+2=t\\2t+2=-t\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}t=-2\left(loại\right)\\t=-\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow a^2-2a=-\dfrac{2}{3}\Leftrightarrow a^2-2a+\dfrac{2}{3}=0\)
Người ra đề đam mê với nghiệm xấu thì phải