Tìm số tự nhiên a lớn nhất sao cho 13;15;61 chia a đều dư 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BD
28 tháng 9 2016
1/
12 , 14 , 60 chia hết cho a
mà số lớn nhất thỏa mãn yêu cầu là 2
vì chia hết cho 12 chỉ có : 1 , 2 , 3 , 4 , 6 , 12
14 là : 1 , 2 , 7 , 14
vậy a lớn nhất là 2
2/
42 , 84 , 63 chia hết cho a
a = 3
vì chia hết cho 63 có : 1 , 3 , 9 , ...
42 : 1 , 3 , 6 , 7 , 2 , ....
vì vậy a lớn nhất = 3
28 tháng 12 2020
3)1;4;9;16;25;36;...
4)1;2;3;4;7;11;18;...
5)1;2;5;9;16;27;...
6)0;3;8;15;24;35;...
7)2;5;10;17;26;...
8)1;3;6;10;15;21;28;...
LT
3
TM
17 tháng 7 2016
Bài giải:
- 13 chia a dư 1 => 13-1=12 chia hết cho a
- 15 chia a dư 1 => 15-1=14 chia hết cho a
- 61 chia a dư 1 => 61-1=60 chia hết cho a
=>12;14 và 60 chia hết cho a
=>a\(\in\)ƯC(12;14;60)
Vì a là số tự nhiên lớn nhất => a=ƯCLN(12;14;60)
Ta có: 12=22.3 ; 14=2.7 ; 60=22.3.5
=>ƯCLN(12;14;60)=2
=>a=2
NP
1
NM
1
DN
2
15 tháng 11 2021
Gọi số cần tìm là x
Theo đề, ta có:
13 : x = m+1, 15 : x = m+1, 61 : x = m+1
⟹ x - 1 = ƯCLN(13; 15; 61)
⟹ x - 1 = 3
⟹ x = 2
HD
6
TT
10
TD
7 tháng 8 2016
Giải:
Số tự nhiên a có: 13,15, 61 chia dư 1(lớn nhất)
=>Ta có a>1
Các số: 13;15;61 đều là số lẻ
=> Số đó là số 2( các số khác không số nào thỏa mãn yêu cầu trên)
7 tháng 8 2016
Tao có: 13, 15, 61 chia a đều dư 1
=> a > 1
Mà 13, 15, 61 đều lẻ
=> a = 2(chỉ có a thỏa mãn)
LN
1
3 tháng 11 2019
Theo đề bài ta có :
13 chia x dư 1
15 chia x dư 1 => 13;15;61 chia hết cho x -1
61 chia x dư 1
Vì 13 chia hết cho x-1
15 chia hết cho x-1 => ( a-1) thuộc ƯC( 13;15;61)
61 chia hết cho x-1
Mà a lớn nhất nên a-1 thuộc ƯCLN( 13;15;61)
13=13
15=3.5
61=61
=> UWCLN(13;15;61)=1
=> ta có : x-1=1
<=> x=1 +1
<=> x =2
Vậy x =2
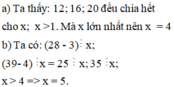
a chia cho 4, 5, 6 dư 1
nên (a - 1) chia hết cho 4, 5, 6
=> (a - 1) là bội chung của (4,5,6)
=> a - 1 = 60n
=> a = 60n+1
với 1 ≤ n < (400-1)/60 = 6,65 mặt khác a chia hết cho 7
=> a = 7m
Vậy 7m = 60n + 1 có 1 chia 7 dư 1
=> 60n chia 7 dư 6 mà 60 chia 7 dư 4
=> n chia 7 dư 5 mà n chỉ lấy từ 1 đến 6
=> n = 5 a = 60.5 + 1 = 301