Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
* Giao điểm với trục Ox:
Ta có: -2x + 3 = 0
⇔ 2x = 3
⇔ x = 3/2
⇒ A(3/2; 0) là giao điểm với trục Ox
* Giao điểm với trục Oy:
x = 0 ⇔ y = 3
⇒ B(0; 3) là giao điểm với trục Oy
* Khoảng cách từ O(0; 0) tới (d):
Xét đồ thị:
Ta có:
AB² = OA² + OB² (Pytago)
= (3/2)² + 3²
= 45/4
⇒ AB = 3√5/2
Khoảng cách từ O đến (d) là đoạn thẳng OH
Ta có:
OH.AB = OA.OB
⇒ OH = OA.OB : AB
= 3/2 . 3 : (3√5/2)
= 3/√5
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
Vậy: (d): y=2x+b
Vì (d) đi qua điểm C(-1;4) nên
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
hay b=6
Vậy: (d): y=2x+6
Thay y=0 vào (d), ta được:
2x+6=0
hay x=-3
Vậy: A(-3;0)
b) Vì y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\b=a+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=\dfrac{-4}{5}+4=\dfrac{-4}{5}+\dfrac{20}{5}=\dfrac{16}{5}\end{matrix}\right.\)
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên ta có: \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
=> (d): y=2x+b
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
\(\Leftrightarrow b=6\)
Vậy: (D): y=2x+6
Thay y=0 vào (d),ta được:
\(2x+6=0\)
\(\Leftrightarrow x=-3\)
Vậy: A(-3;0)
b) Vì đồ thị hàm số y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\-a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=4+a=4+\dfrac{-4}{5}=4-\dfrac{4}{5}=\dfrac{16}{5}\end{matrix}\right.\)
Vậy: \(a=-\dfrac{4}{5}\); \(b=\dfrac{16}{5}\)
c) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(-3-4\right)^2+\left(0-0\right)^2}=7\)(cm)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(-3+1\right)^2+\left(0-4\right)^2}=2\sqrt{5}\left(cm\right)\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(4+1\right)^2+\left(0-4\right)^2}=\sqrt{41}\left(cm\right)\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC\)
\(=7+2\sqrt{5}+\sqrt{41}\)
\(\simeq17,9\left(cm\right)\)
Còn thiếu tính góc tạo bởi đường thẳng BC và trục Ox mà bạn
a: Tọa độ A là:
y=0 và -2x+2=0
=>x=1 và y=0
=>A(1;0)
Tọa độ B là:
x=0 và y=-2x+2
=>x=0 và y=-2*0+2=2
=>B(0;2)
b: C thuộc Ox nên C(x;0)
D thuộc Oy nên D(0;y)
ABCD là hình thoi nên AB=AD và vecto AB=vecto DC
A(1;0); B(0;2); C(x;0); D(0;y)
\(\overrightarrow{AB}=\left(-1;2\right);\overrightarrow{DC}=\left(x;-y\right)\)
\(AB=\sqrt{\left(0-1\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
\(AD=\sqrt{\left(0-1\right)^2+\left(y-0\right)^2}=\sqrt{y^2+1}\)
vecto AB=vecto DC
=>x=-1 và -y=2
=>x=-1 và y=-2
AB=AD
=>y^2+1=5
=>y^2=4
=>y=2(loại) hoặc y=-2(nhận)
Vậy: x=-1 và y=-2
=>C(-1;0); D(0;-2)
Gọi phương trình (d2) có dạng là y=ax+b
(d2) đi qua C và D nên ta có hệ phương trình:
a*(-1)+b=0 và 0*a+b=-2
=>b=-2 và -a=-b=2
=>a=-2 và b=-2
=>y=-2x-2
c: (d1): y=-2x+2 và (d2): y=-2x-2
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x-1=-x+3\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
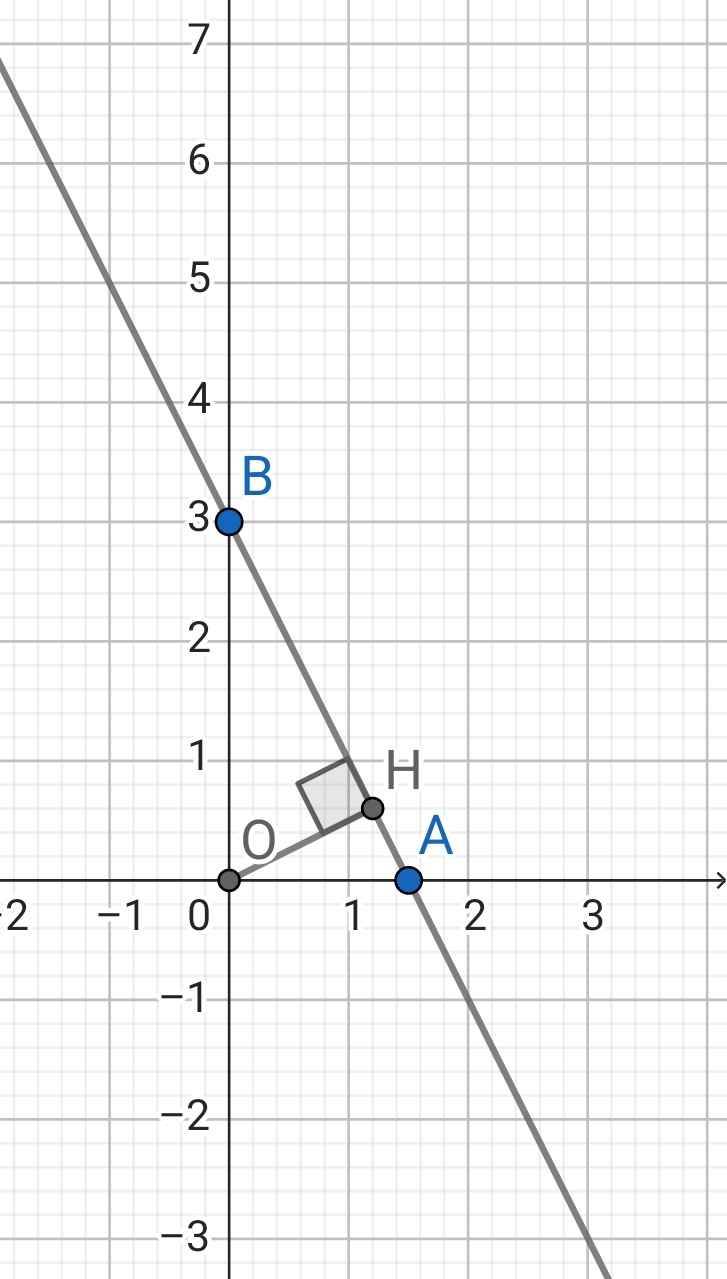
a/ Tọa độ A là nghiệm của hệ
\(\hept{\begin{cases}y=-2x+3\\y=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1,5\\y=0\end{cases}}\)
=> A(1,5; 0)
Tọa độ B là nghiệm của hệ
\(\hept{\begin{cases}x=0\\y=-2x+3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=3\end{cases}}\)
=> B(0; 3)
Khoản cách từ O(0; 0) đến d
\(=\frac{\left|0-2×0-3\right|}{\sqrt{1^2+2^2}}=\frac{3}{\sqrt{5}}\)
b/ Khoản cách từ C(0; - 2) đến d là
\(d\left(C,d\right)=\frac{\left|-2+2×0-3\right|}{\sqrt{1^2+2^2}}=\frac{5}{\sqrt{5}}=\sqrt{5}\)
A/ TỌA ĐỘ A THỎA \(\hept{\begin{cases}Y=0\\Y=-2X+3\end{cases}}\)\(\Rightarrow\Rightarrow A\left(\frac{3}{2},O\right)\)
TỌA ĐỘ B THỎA,\(\hept{\begin{cases}Y=-2X+3\\X=0\end{cases}}\)\(\Rightarrow B\left(0,3\right)\)
GOI H LA HINH CHIEU CUA O LEN (d) ap dung he thuc luong trong tam giac vuongOAB cho
\(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\Leftrightarrow\frac{1}{OH^2}=\frac{1}{\left(\frac{3}{2}\right)^2}+\frac{1}{3^2}\Rightarrow AH=\frac{3}{\sqrt{5}}\)
B/GỌI K LÀ HÌNH CHIẾU CỦA C LÊN (d) ta co\(\frac{OH}{CK}=\frac{OB}{OC}=\frac{3}{5}\Rightarrow CK=\frac{5}{3}OH=\sqrt{5}\)
(....20 NHA)