Tìm hệ số a của đa thức P(x)= a\(x^2-4x-10\), biết rằng đa thức này có một nghiệm là -7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1
4 tháng 5 2017
Vì P(x) có nghiệm bằng 2 => P(2)=0
<=> \(a.2^3\)+\(4.2^2\)- 1 = 0
<=>a = (-15)/8.
TC
22 tháng 5 2022
ta có : \(P\left(\dfrac{-3}{2}\right)=0\)
\(\Leftrightarrow\left(-\dfrac{3}{2}\right)^3-a.\left(-\dfrac{3}{2}\right)^2-2\cdot\dfrac{-3}{2}+4=0\)
\(\Leftrightarrow-\dfrac{27}{8}-\dfrac{9}{4}a+3+4=0\)
\(\Leftrightarrow\cdot\dfrac{9}{4}a=-\dfrac{27}{8}-3-4=-16\)
\(=>a=-16:\dfrac{9}{4}=-\dfrac{64}{9}\)
N
5
4 tháng 5 2017
P(2)= a.23+ 4.22-3.2=0 suy ra 8a+16 -6=0
suy ra 8a= -10
a= -10/8
LL
1
4 tháng 5 2021
Ta có f(x)=ax^2+5x-6 (1)
Thay x=-2 vào (1) ta đc
f(-2)=a(-2)^2+5(-2)-6
= 4a-10-6
=4a-16
Mà x=-2 là 1 nghiệm của f(x)
suy ra 4a-16=0
4a=16
a=4
Vậy a=4
MT
3
DT
1
27 tháng 4 2018
Ta có P(0,5)=0
=>a0,5^2+5.0,5-3=0
=>0,25a+2,5-3=0
=>0,25a-0,5=0
=>0,25a=0,5
=>a=0,5-0,25
a=0,25
Vậy hệ số a là 0,25
TT
18 tháng 4 2021
a/ \(M\left(x\right)=-x^2+5\)
Có \(-x^2\le0\forall x\)
=> \(M\left(x\right)\le5\forall x\)
=> M(x) không có nghiệm.
2/
Thay \(x=\dfrac{1}{2}\) vào đa thức M(x) có
\(M\left(\dfrac{1}{2}\right)=\dfrac{1}{4}a+\dfrac{5}{2}-3=0\)
\(\Leftrightarrow\dfrac{1}{4}a=\dfrac{1}{2}\)
\(\Leftrightarrow a=2\)
Vậy...
J
2
9 tháng 4 2016
P(x) = ax2 + 5x - 3
Đa thức này có một nghiệm là 1/2 tức là P(1/2) = 0
=> a/4 + 5/2 - 3 = 0
=> a = 2
Đáp số: a = 2
9 tháng 4 2016
P(x) = ax^2 + 5x - 3
Đa thức này có một nghiệm là 1/2 tức là P(1/2) = 0
=> a/4 + 5/2 - 3 = 0
=> a = 2
Đáp số: a = 2
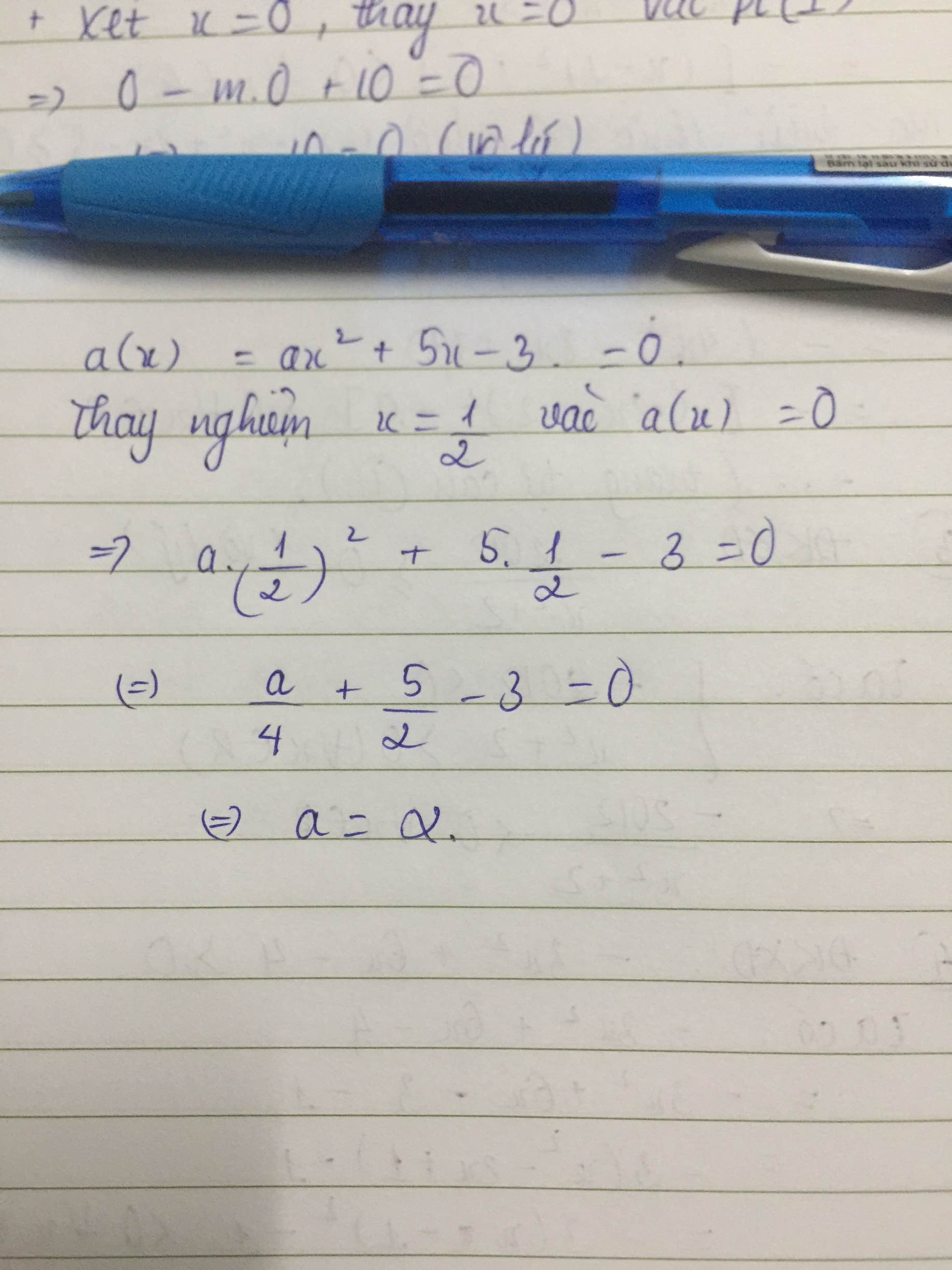
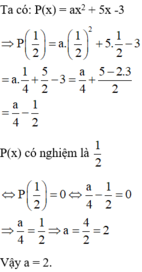
P(-7)=0
=>49a+28-10=0
=>49a+18=0
hay a=-18/49
Đa thức có một nghiệm là `-7`
`=>` Thay `x=-7` vào `P(x)=0` có:
`a.(-7)^2-4.(-7)-10=0`
`=>49a+28-10=0`
`=>49a=-18`
`=>a=-18/49`