Cho \(\widehat{A}\)và \(\widehat{B}\)là hai góc có cạnh tương ứng vuông góc. Biết \(\widehat{A}-\widehat{B}=40^o\), tính số đo các góc A và B.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
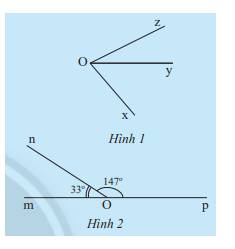
a) Các tia Om, On tương ứng là tia phân giác của góc yOz và xOz vì:
Tia Om nằm trong góc yOz và \(\widehat {yOm} = \widehat {mOz}\)
Tia On nằm trong góc xOz và \(\widehat {xOn} = \widehat {nOz}\)
b) Vì các tia Om, On tương ứng là tia phân giác của góc yOz và xOz nên: \(\widehat {yOm} = \widehat {mOz} = \frac{1}{2}.\widehat {yOz};\widehat {xOn} = \widehat {nOz} = \frac{1}{2}.\widehat {xOz}\)
Mà tia Oz nằm trong góc xOy nên \(\widehat {yOz} + \widehat {xOz} = \widehat {xOy}\)
\( \Rightarrow \widehat {mOz} + \widehat {zOn} = \frac{1}{2}.\widehat {yOz} + \frac{1}{2}.\widehat {xOz} = \frac{1}{2}.\widehat {xOy}\)
Mà tia Oz nằm trong góc mOn nên \(\widehat {mOz} + \widehat {zOn} = \widehat {mOn}\) và \(\widehat {xOy} = 90^\circ \)
\( \Rightarrow \widehat {mOn} = \frac{1}{2}.90^\circ = 45^\circ \)
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) Hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có cạnh Oy chung, không có điểm trong chung
b) Ta có:
\(\begin{array}{l}\widehat {xOy} = 30^\circ ,\widehat {yOz} = 45^\circ ,\widehat {xOz} = 75^\circ \\ \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}\end{array}\)
c) Ta có: \(\widehat {mOn} + \widehat {nOp} = 33^\circ + 147^\circ = 180^\circ \)
4 tháng 2 2021
a) Ta có: \(\widehat{AOB}\) và \(\widehat{BOC}\) là hai góc kề bù(gt)
nên \(\widehat{AOB}+\widehat{BOC}=180^0\)
\(\Leftrightarrow\widehat{AOB}+5\cdot\widehat{AOB}=180^0\)
\(\Leftrightarrow6\cdot\widehat{AOB}=180^0\)
hay \(\widehat{AOB}=30^0\)
Ta có: \(\widehat{BOC}=5\cdot\widehat{AOB}\)(gt)
nên \(\widehat{BOC}=5\cdot30^0\)
hay \(\widehat{BOC}=150^0\)
Vậy: \(\widehat{AOB}=30^0\); \(\widehat{BOC}=150^0\)
b) Trên cùng một nửa mặt phẳng bờ chứa tia OC, ta có: \(\widehat{DOB}< \widehat{BOC}\left(75^0< 150^0\right)\)
nên tia OD nằm giữa hai tia OB và OC
\(\Leftrightarrow\widehat{COD}+\widehat{BOD}=\widehat{COB}\)
\(\Leftrightarrow\widehat{COD}=\widehat{COB}-\widehat{BOD}=150^0-75^0=75^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OC, ta có: \(\widehat{COD}< \widehat{COA}\left(75^0< 180^0\right)\) nên tia OD nằm giữa hai tia OC và OA
\(\Leftrightarrow\widehat{COD}+\widehat{AOD}=\widehat{COA}\)
\(\Leftrightarrow\widehat{AOD}=\widehat{COA}-\widehat{COD}=180^0-75^0\)
hay \(\widehat{AOD}=105^0\)
Vậy: \(\widehat{AOD}=105^0\)
MH
4 tháng 2 2021
a) \(\widehat{AOB}\) và \(\widehat{BOC}\) kề bù \(\Rightarrow\widehat{AOB}+\widehat{BOC}=180^0\) mà \(\widehat{BOC}=5\widehat{AOB}\)
\(\Rightarrow\widehat{AOB}+5\widehat{AOB}=180^0\Rightarrow6\widehat{AOB}=180^0\\ \Rightarrow\widehat{AOB}=30^0\Rightarrow\widehat{BOC}=150^0\).
b) Do \(OD\) nằm trong góc \(\widehat{BOC}\) \(\Rightarrow\) tia \(OD\) nằm giữa hai tia \(OB,OC\)
\(\Rightarrow\)tia \(OB\) và tia \(OA\) nằm cùng phía nhau so với tia \(OD\)
\(\Rightarrow\) tia \(OB\) nằm giữa hai tia \(OA,OD\)
\(\Rightarrow\widehat{AOD}=\widehat{AOB}+\widehat{BOD}=30^0+75^0=105^0\).
c) Nếu chỉ xét trường hợp các góc tạo bởi hai tia liên tiếp nhau:
Trên nửa mặt phẳng bờ \(AC\) có \(n+4\) tia (gồm \(4\) tia \(OA,OB,OC,OD\) và \(n\) tia vẽ thêm).
Cứ hai tia cạnh nhau tạo thành 1 góc
\(\Rightarrow\) Ta có \(n+3\) góc.
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
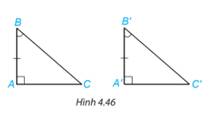
Xét 2 tam giác ABC và A'B'C' có:
\(\widehat B = \widehat {B'}\) (gt)
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(g.c.g)
15 tháng 9 2021
Vì \(\widehat{A}-\widehat{B}=\widehat{B}-\widehat{C}\) nên \(\widehat{A}-2\widehat{B}+\widehat{C}=0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A}-2\widehat{B}+\widehat{C}=0^0\left(1\right)\\\widehat{A}+\widehat{B}+\widehat{C}=180^0\left(2\right)\end{matrix}\right.\)
Trừ \(\left(2\right)\) cho \(\left(1\right)\), ta được \(3\widehat{B}=180^0\Rightarrow\widehat{B}=60^0\)
\(\Rightarrow\widehat{A}+\widehat{C}=120^0\)
Vậy GTLN của \(\widehat{A}\) là \(119^0\) vì \(\widehat{C}>0\)
B1
16 tháng 9 2017
làm tương tự
Bài 1 Cho tam giác ABC có góc A= 40 độ,AB=AC.Gọi M Là trung điểm của BC tính các góc của mỗi tam giác AMB và tam giác AMC
bài làm
Bài 1:
-Vì M là trung điểm nên CM=BM
-Vì AM chung và theo GT AB=AC nên Tam giác ABM=tam giac ACM
Góc A=40 độ=>Góc MAB=MAC=20
Vì góc AMB+góc AMC=180 độ(2 góc kề bù) mà góc AMB=AMC nên AMB=AMC=90 độ(2 góc tương ứng)
=>góc ABM=góc ACM=70 độ
Vậy Góc A=Góc C=70 độ
Góc AMC=góc AMB=90 độ
Góc CAM=góc BAM=20 độ
Thanks nhá
20 tháng 11 2017
Theo đề ra ta có :
\(\Rightarrow\hept{\begin{cases}A-B=40^o\\A+B=90^o\end{cases}}\)
Góc A sẽ bằng:
(90 + 40) :2 = 65o
Góc B sẽ bằng :
90o - 65o = 25o
Vậy ...............
20 tháng 11 2017
Theo de bai ta co :
A-B=40°
A+B=90°
Goc A se bang :
(90+40):2=65°
Goc B se bang :
90°-65°=25°
Dap so : ......
Theo đề ra ta có
\(\hept{\begin{cases}A-B=40\\A+B=90\end{cases}\Leftrightarrow\hept{\begin{cases}A=40+B\\40+B+B=90\end{cases}}}\)
\(\Rightarrow B=25\)
\(\Rightarrow A=65\)
Do 2 góc của một tam giác vuông nên bằng 90 độ đó na