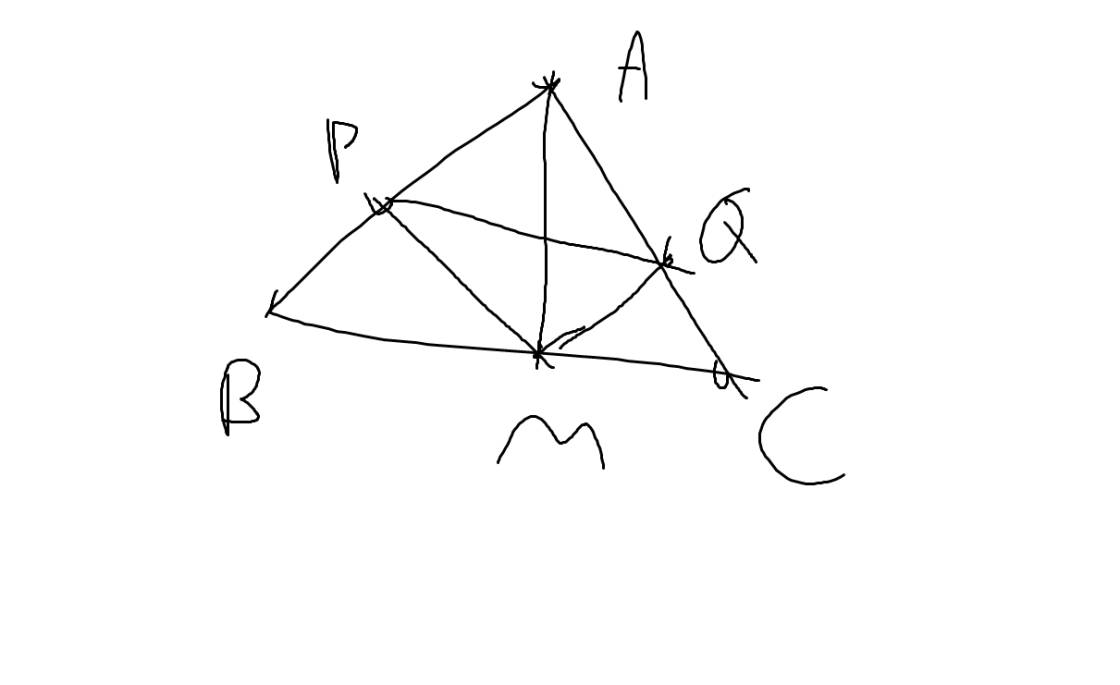
Cho \(\Delta ABC\) cân tại A. Từ 1 điểm tùy ý trên cạnh BC. Kẻ MP vuông góc với AB \(\left(P\in AB\right)\)và MQ vuông góc với AC \(\left(Q\in AC\right)\). Khi M di chuyển trên cạnh BC thì MP+MQ không đổi.
Em hãy chứng tỏ điều trên bằng những kiến thức đã học ở chương TỨ GIÁC.