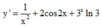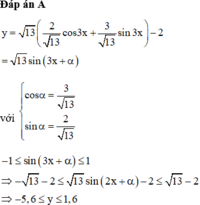tìm nguyên hàm của hàm số y=sin(3x-2) Giúp mik với nha.:)))
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 8 2023
a: \(y'=\left(sin3x\right)'+\left(sin^2x\right)'=3\cdot cos3x+sin\left(x+pi\right)\)
b: \(y'=\left(log_2\left(2x+1\right)\right)'+\left(3^{-2x+1}\right)'\)
\(=\dfrac{2}{\left(2n+1\right)\cdot ln2}-2\cdot3^{-2x+1}\cdot ln3\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
\(y'=\left(sin3x\right)'=3cos3x\)
\(\Rightarrow y''=-9sin3x\)
17 tháng 8 2023
tham khảo:
a)\(y'=xsin2x+sin^2x\)
\(y'=sin^2x+xsin2x\)
b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)
c)\(y=sin3x-3sinx\)
\(y'=3cos3x-3cosx\)
d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)
\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)
13 tháng 10 2021
Đặt y = ax + 4 (d) ; y = -3x (d1)
d // d1 <=> \(\hept{\begin{cases}a=-3\\4\ne0\end{cases}}\Leftrightarrow a=-3\)
b, Thay x = 1 ; y = 6 vào (d) ta được : \(a+4=6\Leftrightarrow a=2\)
