Cho tam giác ABC vuông tại A và ABC bằng 60 độ
a) so sánh AB và AC
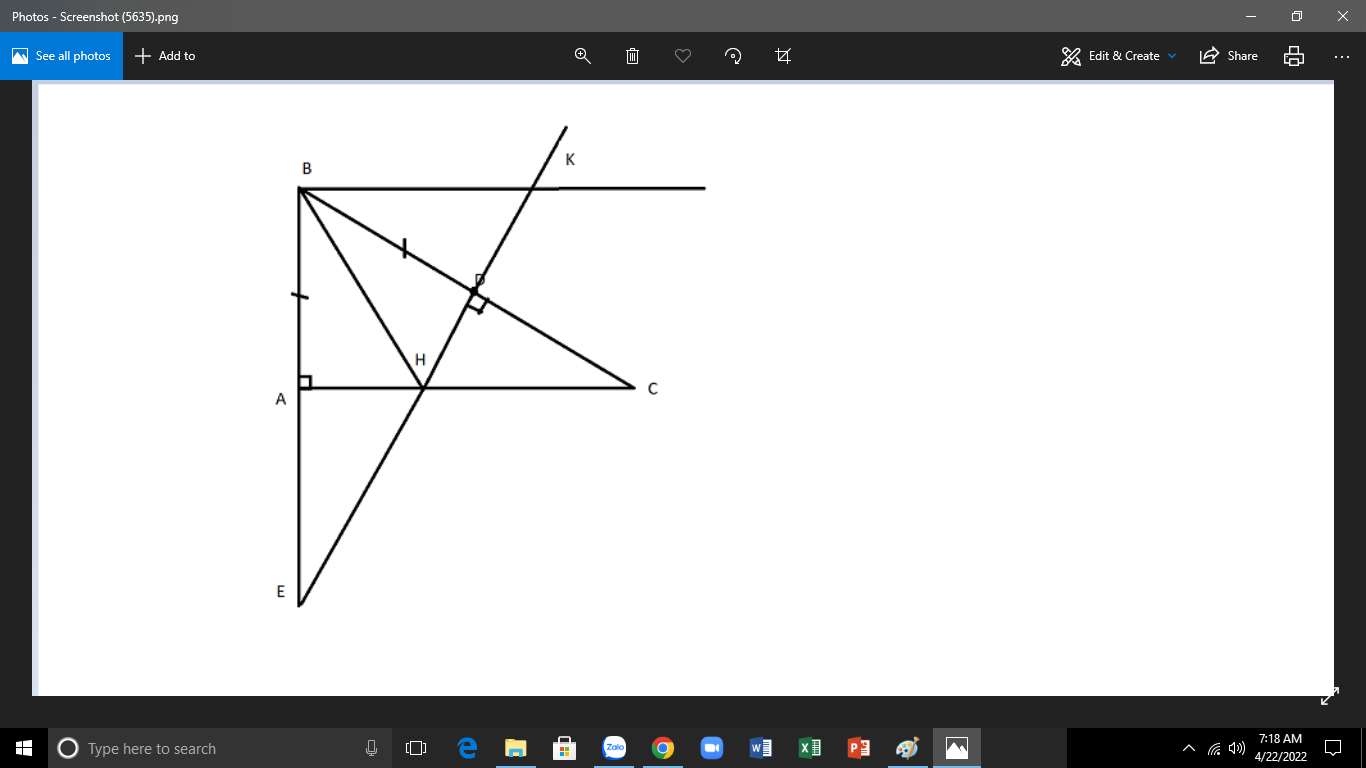
b) trên cạnh BC lấy điểm D sao cho BD = AB qua D kẻ đường thẳng vuông góc với BC cắt tia đối tia AE Chứng minh tam giác ABC =tam giác DBE
c) Gọi H là giao điểm của AD và AC . Chứng minh BH là đường phân giác của ABC
d) qua B đoạn đường thẳng vuông góc với AB cắt đường thẳng AB tại K. Chứng minh tam giác HBK đều



a: \(\widehat{ACB}=90^0-60^0=30^0\)
XétΔABC có \(\widehat{ACB}< \widehat{ABC}\)
nên AB<AC
b: Xét ΔBAC vuông tại A và ΔBDE vuông tại D có
BA=BD
góc ABC chung
Do đó;ΔBAC=ΔBDE
c: Xét ΔBAH vuông tại A và ΔBDH vuông tại D có
BH chung
BA=BD
DO đó:ΔBAH=ΔBDH
SUy ra: \(\widehat{ABH}=\widehat{DBH}\)
hay BH là phân giác của góc ABC