GIÚP MÌNH VỚI NHA!!! LÀM ƠN!
Cho hình thoi ABCD có góc A = 60o. Hãy tính tỉ số \(\frac{AC^2}{AB^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 8 2023
1) \(S_{ABCD}=\dfrac{1}{2}.AC.BD\Rightarrow BD=\dfrac{2S_{ABCD}}{AC}=\dfrac{2.50\sqrt[]{3}}{10}=10\sqrt[]{3}\left(cm\right)\)
Gọi O là giao điểm AC và BD
\(\Rightarrow\left\{{}\begin{matrix}OA=\dfrac{1}{2}AC=5\left(cm\right)\\OB=\dfrac{1}{2}BD=5\sqrt[]{3}\left(cm\right)\end{matrix}\right.\)
Xét Δ vuông OAB có :
\(AB^2=OA^2+OC^2=25+25.3=100\left(cm^2\right)\left(Pitago\right)\)
\(\Rightarrow AB=10\left(cm\right)\)
2) Xét Δ vuông OAB có :
\(AB=2OA=10\left(cm\right)\)
⇒ Δ OAB là Δ nửa đều
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABD}=30^o\\\widehat{BAC}=60^o\end{matrix}\right.\)
mà \(\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2\widehat{BAC}\\\widehat{ADC}=\widehat{ABC}=2\widehat{ABD}\end{matrix}\right.\) (tính chất hình thoi)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2.60=120^o\\\widehat{ADC}=\widehat{ABC}=2.30=60^o\end{matrix}\right.\)
6 tháng 3 2022
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE
=>ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔBAE đều
c: Xét ΔABC vuông tại A có
\(\tan B=\dfrac{AC}{AB}\)
\(\Leftrightarrow AC=5\sqrt{3}\left(cm\right)\)
PH
0
CM
2 tháng 6 2017
Đáp án là C
Gọi H là hình chiếu của A’ trên (ABCD). Dễ thấy góc
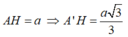
Dễ dàng tính được diện tích đáy
25 tháng 2 2016
ABC =300 cm
ADC=600 cm
thông cảm cho mình nha ko biết gõ kí hiệu vuông
25 tháng 2 2016
Minh khong biet
Mình mới học lớp 4
Đáp số:Minh moi hoc lop 4
30 tháng 12 2018
c,
- Gọi O là giao điểm của AC và BD.
- AB//CD nên góc BAC = góc ACD (so le trong), tương tự góc ABD=góc BDC.
- Theo đề bài góc ACD=gócBDC nên góc BAC=góc ABD.
=>Tam giác ABO cân tại O => 0A=0B.(1)
Tương tự tam giác ODC cân tại O =>OD=OC.(2)
Lại có góc AOD=góc BOC (đối đỉnh ) (3)
Từ (1), (2), (3) suy ra tam giác AOD = tam giác OBC nên suy ra :
+ AD=BC (*)
+ Góc ADB=góc BCA(**)
Từ (*) và (**) suy ra hình thang ABCD cân(hình thang có hai cạnh bên bằng nhau và hai góc ở đáy bằng nhau )
Gọi giao điểm hai đường chéo hình thoi là I
Vì hình thoi có góc A =60 nên tam giác ABD đều => AB = AD = DB
Ta có AC = 2AI
\(AI^2=AB^2-BI^2=AB^2-\frac{BD^2}{4}=AB^2-\frac{AB^2}{4}=\frac{3AB^2}{4}\)
\(\Rightarrow\frac{AC^2}{AB^2}=\frac{4AI^2}{AB^2}=\frac{4\frac{3AB^2}{4}}{AB^2}=3\)
cảm ơn bạn nhiều nhé! Bạn giỏi quá à!