Chứng minh rằng số 2005^2 +2^2005 và 2005 nguyên tố cùng nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
1
17 tháng 12 2016
2005 se có tận cùng là 5
Vì các số 2 mũ luôn có số tận cùng lần lượt là 2;4;6;8
ta có:
2005:4=501 dư 1 suy ra tận cùng là chữ số 2 : 5+2=7
Vì 2005 không chia hết cho 3 hay 9
Mà các số tận cùng là 7 và 5
suy ra 2 số trên là 2 số nguyên tố cùng nhau
NT
4
DT
13 tháng 3 2017
mày lấy vì 2006^2005 +và -1 >3
xét 3 số tự nhiên liên tiếp luôn có 1 số chia hết cho 3
vì 2006 không chia hết cho 3, 3 là số nguyên tố
2006^2005 không chia hết cho 3
2006^2005-1 hoặc 2006^2005+1 chia hết co 3
tự tiếp k nha
18 tháng 7 2015
Hằng đẳng thức a2 - b2 = (a - b).(a + b) <=> (a - b).(a + b) = a2 - b2
CM
23 tháng 8 2017
(Ghi chú: Muốn chứng minh hai số là nghịch đảo của nhau, ta chứng minh tích của hai số bằng 1.)
5 tháng 9 2021
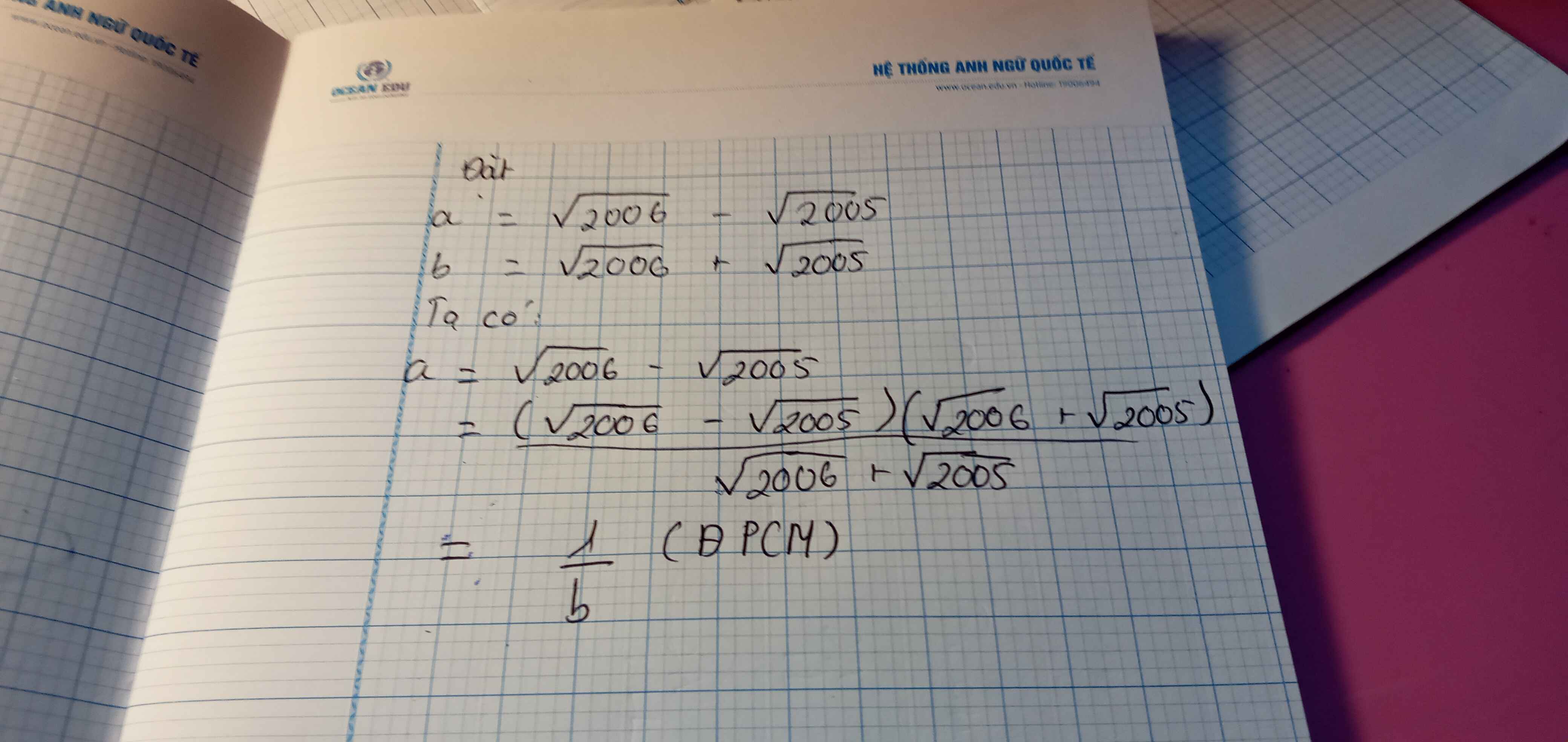
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)
Ta có
\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)
\(\RightarrowĐfcm\)
2005 sẽ có tận cùng là 5
vì các số 2 mũ luôn có tận cùng lần lượt là 2,4,8,6
ta có 2005/4=501 dư1 =>tận cùng là chữ số 2
5+2=7
vì 2005 ko chia hết cho 3 hay 9
mà các số có tận cùng là 7 và 5
\(\Rightarrow\)2 số trên là thừa số nguyên tố
quên mất 2 thừa số nguyên tố cùng nhau