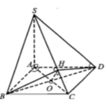
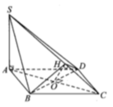
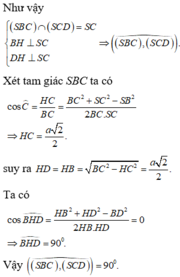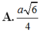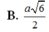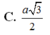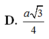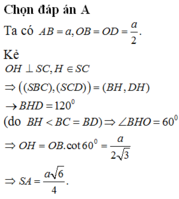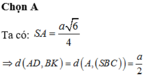Cho hình chóp S. ABCD có đáy là hình thoi cạnh a, Góc ABC =120°, SA vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60. Tính SA Mọi người giúp em với ạ!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 6 2021
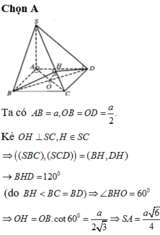
Dễ dàng chứng minh \(BD\perp\left(SAC\right)\Rightarrow BD\perp SC\)
Gọi O là tâm đáy, kẻ \(OH\perp SC\Rightarrow SC\perp\left(BDH\right)\)
\(\Rightarrow\widehat{BHD}\) hoặc góc bù của nó là góc giữa (SBC) và (SCD) \(\Rightarrow\widehat{BHD}=60^0\) hoặc \(120^0\)
\(\Rightarrow\widehat{BHO}\) bằng \(30^0\) hoặc \(60^0\)
Tam giác ABD đều \(\Rightarrow BD=a\) \(\Rightarrow OB=\dfrac{a}{2}\)
TH1: \(\widehat{BHO}=30^0\)
\(\Rightarrow OH=\dfrac{OB}{tan30^0}=\dfrac{a\sqrt{3}}{2}=OC\Rightarrow\Delta\) vuông OCH có cạnh huyền bằng cạnh góc vuông (loại)
TH2: \(\widehat{BHO}=60^0\Rightarrow OH=\dfrac{OB}{tan60^0}=\dfrac{a\sqrt{3}}{6}\)
\(\Rightarrow SA=AC.tan\widehat{SCA}=AC.\dfrac{OH}{\sqrt{OC^2-OH^2}}=\dfrac{a\sqrt{6}}{4}\)
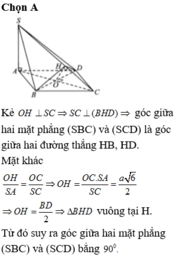
Từ A kẻ \(AM\perp SB\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM=d\left(A;\left(SBC\right)\right)\)
\(AD||BC\Rightarrow AD||\left(SBC\right)\Rightarrow d\left(BK;AD\right)=d\left(AD;\left(SBC\right)\right)=d\left(A;\left(SBC\right)\right)=AM\)
\(\dfrac{1}{AM^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{11}{3a^2}\Rightarrow AM=\dfrac{a\sqrt{33}}{11}\)
22 tháng 2 2021
gọi K thuộc SC sao cho DK \(\perp\) SC , BK \(\perp\)SC
=> ((SCD),(SBC)) = (DK,KB)
tính được SD = \(\frac{\sqrt{10}}{2}\)a, AC = \(\sqrt{3}\)a, SC= \(\frac{3\sqrt{2}}{2}\)a
\(DC^2=SD^2+SC^2-2SD.SC.cos\widehat{DSC}\)
=> \(\widehat{DSC}\)=....... (số xấu)
\(sin\widehat{DSC}\)= \(\frac{DK}{SD}\)=> DK = \(\frac{\sqrt{2}}{2}\)=BK
\(DB^2=DK^2+BK^2-2.DK.BK.cos\alpha\)=> \(\alpha=\frac{\pi}{2}\)
