* Mọi người giúp mik với ạ! *
Tìm a lớn nhất để bất phương trình sau thỏa mãn ∀x ∈ [0;1]
a(x ² + x - 1) ≤ (x ² + x - 1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 5 2022
bài này hình như sai đề ấy nhỉ, thử thay x=0 vào thì bt thỏa mãn khi a≥1, vậy thì làm gì có đáp án nhỉ :3
17 tháng 5 2022
(1- a)( x +x -1)\(\ge\) 0
xem hình vẽ parabol (x + x - 1) , trong khoảng [0,1] thì luôn âm, muốn bất đẳng thức dương thì ( 1 - a) phải âm.
1 - a ≤ 0
1 ≤ a ≤ + ∞
a nhỏ nhất là 1. còn lớn nhất là số dương không xác định.
AH
Akai Haruma
Giáo viên
3 tháng 4 2022
Lời giải:
Để pt có 2 nghiê pb thì:
$\Delta'=1-(m-3)>0\Leftrightarrow m< 4$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2\\ x_1x_2=m-3\end{matrix}\right.\)
Khi đó:
\(x_1^2-2x_2+x_1x_2=-12\)
\(\Leftrightarrow x_1^2-2(2-x_1)+x_1(2-x_1)=-12\)
\(\Leftrightarrow x_1=-2\Leftrightarrow x_2=2-x_1=4\)
$m-3=x_1x_2=(-2).4=-8$
$\Leftrightarrow m=-5$ (tm)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 2 2021
1.
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)
2.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)
Không tồn tại m thỏa mãn
CM
14 tháng 11 2019
Chọn B
Phương pháp: Đánh giá.
Cách giải: Với x=1 dễ thấy bất phương trình thỏa mãn với mọi m
Do đó yêu cầu bài toán tương đương với
PT
1
CM
30 tháng 5 2017
Ta có: 5,2 + 0,3x < - 0,5
⇔ 0,3x < - 0,5 – 5,2
⇔ 0,3x < - 5,7
⇔ x < -19
Vậy số nguyên lớn nhất cần tìm là -20
CM
22 tháng 7 2018
Chọn D
Ta có: ( 2m+1) x+ m-5 ≥ 0 tương đương: ( 2m+ 1) x≥ 5- m (*)
+ TH1: Với m> -1/2 , bất phương trình (*) trở thành: 
Tập nghiệm của bất phương trình là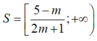 
Để bất phương trình đã cho nghiệm đúng với 0< x< 1 thì 
Hay 
+ TH2: m= -1/ 2, bất phương trình (*) trở thành: 0x ≥ 5+ 1/2
Bất phương trình vô nghiệm. Nên không có m thỏa mãn
+ TH3: Với m< -1/ 2 , bất phương trình (*) trở thành: 
Tập nghiệm của bất phương trình là 
Để bất phương trình đã cho nghiệm đúng với 0< x < 1thì 
Hay 
Kết hợp điều kiện m< -1/ 2 nên không có m thỏa mãn.
Vậy với m ≥ 5, bất phương trình đã cho nghiệm đúng với mọi x: 0< x< 1