Cho hình thang ABCD (AB//CD); AB < CD). Kẻ AP vuông góc với CD (P thuộc CD), BQ vuông góc với đường chéo AC (Q thuộc AC). Chứng minh: tam giác APC ~ tam giác BQA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
2
10 tháng 8 2021
a,
ABCD là hình thang cân \(=>\angle\left(CAB\right)=\angle\left(DBA\right)\)
=>2 góc ngoài cũng bằng nhau
=>2 tia phân giác 2 góc ngoài cũng tạo thành các góc bằng nhau
\(=>\angle\left(EAB\right)=\angle\left(FBA\right)\)=>ABFE là hình thang cân
b,từ 2 điểm A,B hạ các đường cao AM,BN
chứng minh được AMNB là h chữ nhật
=>MN=AB=6cm
dễ chứng minh được tam giác ADM=tam giác BCN(ch-cgn)
\(=>DM=CN=\dfrac{1}{2}\left(DC-MN\right)=\dfrac{1}{2}\left(12-6\right)=3cm\)
pytago=>\(BN=\sqrt{BC^2-NC^2}=\sqrt{5^2-3^2}=4cm\)
\(=>SABCD=\dfrac{BN\left(AB+CD\right)}{2}=........\)thay số tính
22 tháng 6 2015
từ A kẻ đường thẳng song song với BC cắt CD tại E
\(\Rightarrow\) Tứ giác ABCE là hình bình hành \(\Rightarrow AB=CE=4cm;AE=BC=5cm\)\(\Rightarrow DE=CD-EC=4cm\)
xét tam giác ADE có AD2+ DE2 = 32 + 42 = 25; AE2 = 52 =25 \(\Rightarrow AD^2+DE^2=AE^2\)\(\Rightarrow\Delta ADE\) vuông tại D \(\Rightarrow AD\) Vuông góc với DE hay AD vuông góc với DC suy ra tứ giác ABCD là hình thang vuông
27 tháng 9 2021
Xét ΔOAB có OA=OB
nên ΔOAB cân tại O
Suy ra: \(\widehat{OAB}=\widehat{OBA}\)
mà \(\widehat{OAB}=\widehat{OCD}\)
và \(\widehat{OBA}=\widehat{ODC}\)
nên \(\widehat{OCD}=\widehat{ODC}\)
Xét ΔODC có \(\widehat{OCD}=\widehat{ODC}\)
nên ΔODC cân tại O
Suy ra: OD=OC
Ta có: OA+OC=AC
OB+OD=BD
mà OA=OB
và OC=OD
nên AC=BD
Xét hình thang ABCD có AC=BD
nên ABCD là hình thang cân
PT
28 tháng 11 2021
a, Xét tam giác ADC có Q là trung điểm của AD và P là trung điểm của DC => QP là đường trung bình của tam giác ADC.=> QP//AC và QP=\(\dfrac{1}{2}\)AC (1)
Xét tam giác ABC có M là trung điểm của AB và N là trung điểm của BC => MN là đường trung bình của tam giác ABC => MN//AC và MN=\(\dfrac{1}{2}\)AC (2)
Từ (1) và (2) => QP=MN và QP//MN => MNPQ là hình bình hành
b,Nếu ABCD là hình thang cân <=> AC=BD (2 đường chéo) (3)
Xét tam giác BCD có N là trung điểm của BC và P là trung điểm của DC => NP là đương trung bình của tam giác BCD => NP//BD và NP=\(\dfrac{1}{2}\)BD (4)
=> Từ (1) (3) và (4) ta có QP=NP
=> ABCD là hình bình hành có QP=NP ( cạnh kề )
=> ABCD là hình thoi
BẠN TỰ VẼ HÌNH NHA
AT
29 tháng 6 2021
Kẻ \(AE,BF\bot CD\)
Vì \(AE\parallel BF(\bot CD),AB\parallel EF\) (ABCD là hình thang cân)
\(\Rightarrow ABFE\) là hình bình hành có \(\angle AEF=90\Rightarrow ABFE\) là hình chữ nhật
\(\Rightarrow AB=FE\)
Dễ dàng chứng minh được \(DE=CF\left(\Delta ADE=\Delta BFC\right)\)
\(\Rightarrow DE=\dfrac{CD-AB}{2}=\dfrac{7-3}{2}=2\)
\(\Rightarrow AE=\sqrt{AD^2-DE^2}=\sqrt{5^2-2^2}=\sqrt{21}\)
\(\Rightarrow S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).AE=\dfrac{1}{2}\left(7+3\right).\sqrt{21}=5\sqrt{21}\)
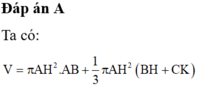
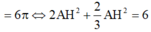
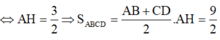
Xét \(2\Delta:\Delta APC\) và \(\Delta BQA\) có:
\(\left\{{}\begin{matrix}\widehat{APC}=\widehat{BQA}=90^o\\\widehat{BAQ}=\widehat{ACP}\left(slt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta APC\sim\Delta BQA\left(g-g\right)\)