Phân tích đa thức thành nhân tử x2 -y2-4x-2y+3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: x2 – y2 – 2y - 1 = x2 – (y2 + 2y + 1)
= x2 – (y + 1)2
= (x + y + 1).(x - y - 1)
Chọn D

x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) → bạn Việt dùng phương pháp nhóm hạng tử
= (x - y)2 + 4(x – y) → bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) → bạn Việt dùng phương pháp đặt nhân tử chung

`x^2+2x+1-y^2+2y-1`
`=(x^2+2x+1)-(y^2-2y+1)`
`=(x+1)^2-(y-1)^2`
`=(x+1+y-1)(x+1-y+1)`
`=(x+y)(x-y+2)`
Ta có: \(x^2+2x+1-y^2+2y-1\)
\(=\left(x+1\right)^2-\left(y-1\right)^2\)
\(=\left(x+1-y+1\right)\left(x+1+y-1\right)\)
\(=\left(x-y+2\right)\left(x+y\right)\)

2x – 2y – x2 + 2xy – y2
(Có x2 ; 2xy ; y2 ta liên tưởng đến HĐT (1) hoặc (2))
= (2x – 2y) – (x2 – 2xy + y2)
= 2(x – y) – (x – y)2
(Có x – y là nhân tử chung)
= (x – y)[2 – (x – y)]
= (x – y)(2 – x + y)

Nhận thấy x2 + 4x + 4 là hằng đẳng thức nên ta nhóm với nhau.
x2 + 4x – y2 + 4
= (x2 + 4x + 4) – y2
= (x + 2)2 – y2 (Xuất hiện hằng đẳng thức (3))
= (x + 2 – y)(x + 2 + y)

x^2+4x-2xy-4y+y^2=(x^2-2xy+y^2)+(4x-4y)
=(x-y)^2+4(x-y)
=(x-y)(x-y+4)

a) \(x^2-y^2-3x+3y\)
\(=\left(x-y\right)\left(x+y\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-3\right)\)
b) \(2x+2y-x^2+y^2\)
\(=2\left(x+y\right)-\left(x^2-y^2\right)\)
\(=2\left(x+y\right)-\left(x-y\right)\left(x+y\right)\)
\(=\left(x+y\right)\left(2-x+y\right)\)
c) \(x^2-16+y^2+2xy\)
\(=x^2+y^2+2xy-16\)
\(=\left(x+y\right)^2-16\)
\(=\left(x+y+4\right)\left(x+y-4\right)\)
a) \(x^2-y^2-3x+3y\)
\(=\left(ax+y\right)\left(ax-y\right)-3.\left(x-y\right)\)
b) \(2x+2y-x^2+y^2\)
\(=2\left(x+y\right)-\left(x+y\right)\left(x-y\right)\)
c) \(x^2-16+y^2+2xy\)
\(=\left(x+y\right)\left(x-y\right)+2xy-16\)

\(=x^2-\left(y+1\right)^2=\left(x-y-1\right)\left(x+y+1\right)\)
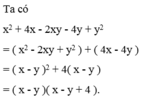
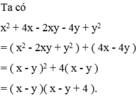
x2-y2-4x-2y+3=(x2-4x+4)-(y2+2y+1)=(x-2)2-(y+1)2=(x-2+y+1)(x-2-y-1)
\(x^2-y^2-4x-2y+3\)
\(=\left(x^2-4x+4\right)-\left(y^2+2y+1\right)\)
\(=\left(x-2\right)^2-\left(y+1\right)^2\)
\(=\left(x-2-y-1\right)\left(x-2+y+1\right)\)
\(=\left(x-y-3\right)\left(x+y-1\right)\)