C = 75 . ( $4^{2019}$ + $4^{2018}$ + $4^{2017}$ + ... + $4^{2}$ + 4 +1 ) + 25
Chứng tỏ C chia hết cho 100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
0
NM
1
DK
7 tháng 1 2016
đặt biểu thức ban đầu là A, 42020+42019+...+4+1=B
4B=42021 +42020 +42019+...+42+4
3B=4B-B=42021-1 => B= (42021-1)/3
A=75B+25=75(42021-1)/3 + 25= 25(42021-1)+25=25(42021-1+1)=25.42021=100.42020
=> A chia hết cho cả 100 và 42021
mặt khác A=25.42021=42021.(24+1)=24.42021+42021=6.42022+42021
vì 42021<42022 nên A chia 42022 dư 42021
tick cho mk nha!!!!!!!!
NN
29 tháng 12 2017
Câu 2:
\(C=3^{10}+3^{11}+3^{12}+...+3^{17}.\)
\(C=\left(3^{10}+3^{11}+3^{12}+3^{13}\right)+\left(3^{14}+3^{15}+3^{16}+3^{17}\right).\)
\(C=3^{10}\left(1+3+3^2+3^3\right)+3^{14}\left(1+3+3^2+3^3\right).\)
\(C=3^{10}\left(1+3+9+27\right)+3^{14}\left(1+3+9+27\right).\)
\(C=3^{10}.40+3^{14}.40.\)
\(C=\left(3^{10}+3^{14}\right).40⋮40\left(đpcm\right).\)
NT
29 tháng 12 2017
\(C=3^{10}+3^{11}+..+3^{17}\\ =\left(3^{10}+3^{11}+3^{12}+3^{13}\right)+\left(3^{14}+..+3^{17}\right)\\ =3^{10}\left(1+3+3^2+3^3\right)+3^{14}\left(1+3+3^2+3^3\right)\\ =40\left(3^{10}+3^{14}\right)⋮40\)
P
3
SP
1
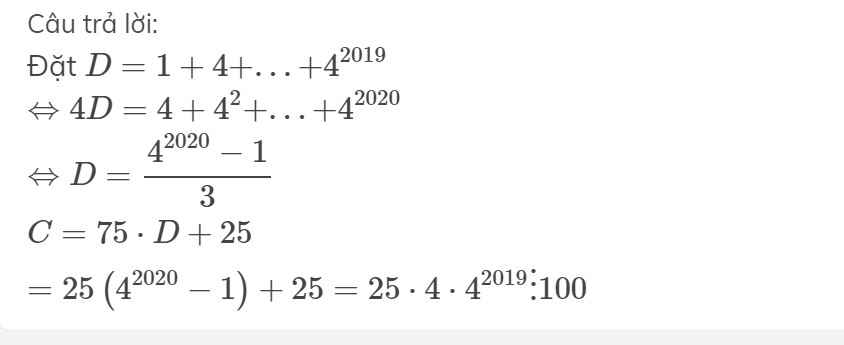
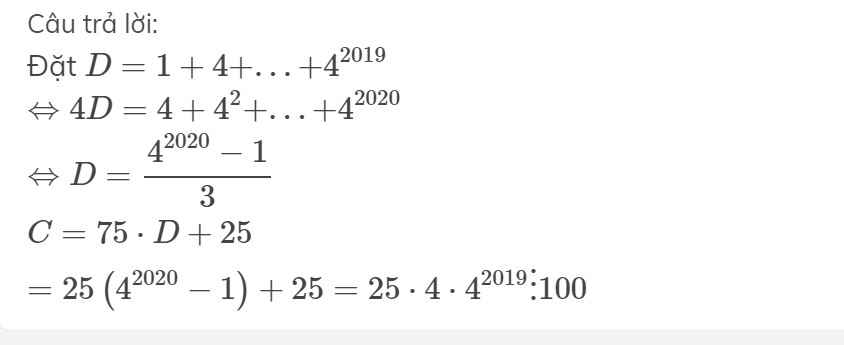
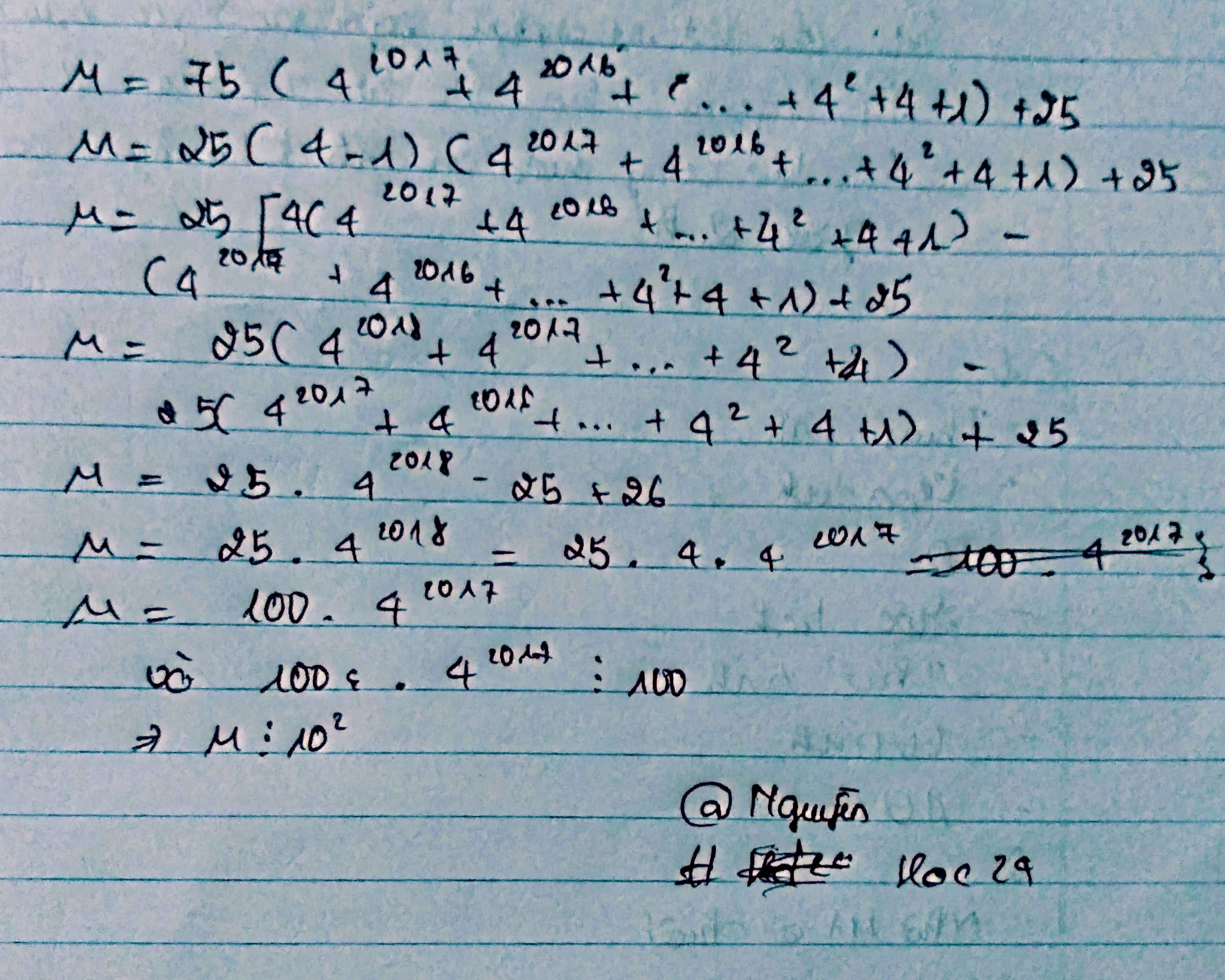
Đặt \(D=1+4+...+4^{2019}\)
\(\Leftrightarrow4D=4+4^2+...+4^{2020}\)
\(\Leftrightarrow D=\dfrac{4^{2020}-1}{3}\)
\(C=75\cdot D+25\)
\(=25\left(4^{2020}-1\right)+25=25\cdot4\cdot4^{2019}⋮100\)