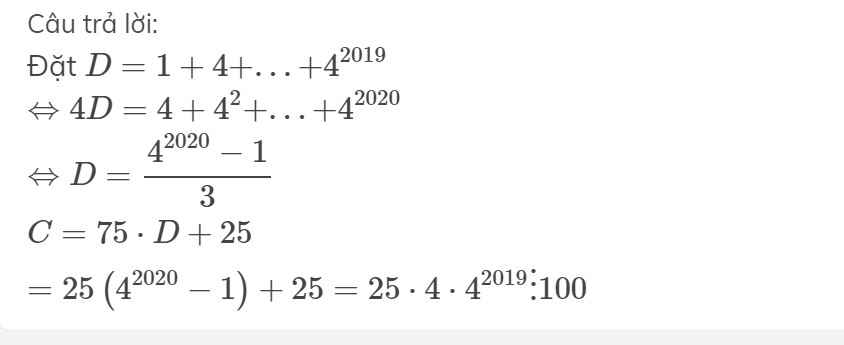Cho C = 75 . ( $4^{2019}$ + $4^{2018}$ + $4^{2017}$ + ... + $4^{2}$ + 4 +1 ) + 25
Chứng tỏ C chia hết cho 100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
12 tháng 5 2022
Đúng(1)
Những câu hỏi liên quan
12 tháng 5 2022
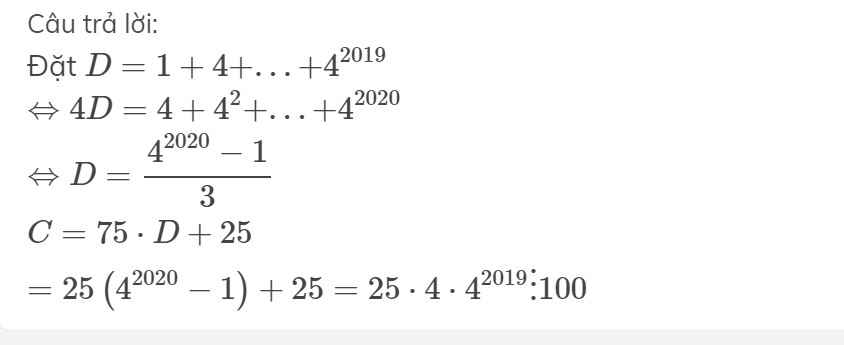
Đặt \(D=1+4+...+4^{2019}\)
\(\Leftrightarrow4D=4+4^2+...+4^{2020}\)
\(\Leftrightarrow D=\dfrac{4^{2020}-1}{3}\)
\(C=75\cdot D+25\)
\(=25\left(4^{2020}-1\right)+25=25\cdot4\cdot4^{2019}⋮100\)
TH
0
DK
7 tháng 1 2016
đặt biểu thức ban đầu là A, 42020+42019+...+4+1=B
4B=42021 +42020 +42019+...+42+4
3B=4B-B=42021-1 => B= (42021-1)/3
A=75B+25=75(42021-1)/3 + 25= 25(42021-1)+25=25(42021-1+1)=25.42021=100.42020
=> A chia hết cho cả 100 và 42021
mặt khác A=25.42021=42021.(24+1)=24.42021+42021=6.42022+42021
vì 42021<42022 nên A chia 42022 dư 42021
tick cho mk nha!!!!!!!!
SP
1
19 tháng 8 2017
a, Ta có: \(4\equiv1\left(mod3\right)\)
\(\Rightarrow4^{2018}\equiv1\left(mod3\right)\)
\(\Rightarrow4^{2018}-1⋮3\)
b, Ta có: \(5\equiv1\left(mod4\right)\)
\(\Rightarrow5^{2019}\equiv1\left(mod4\right)\)
\(\Rightarrow5^{2019}-1⋮4\)
c, \(4\equiv-1\left(mod5\right)\)
\(\Rightarrow4^{2019}\equiv-1\left(mod5\right)\)
\(\Rightarrow4^{2019}+1⋮5\)
d, \(5\equiv-1\left(mod6\right)\)
\(\Rightarrow5^{2017}\equiv-1\left(mod6\right)\)
\(\Rightarrow5^{2017}+1⋮6\)
PT
19 tháng 8 2017
1. Vì \(4\) chia \(3\) dư \(1\)
\(\Rightarrow4^{2018}\) chia \(3\) dư \(1^{2018}=1.\)
\(\Rightarrow4^{2018}-1\) chia hết cho \(3.\)
TV
0