Tìm các số hữu tỉ m và n; biết rằng hiệu của n và m bằng thương của n và m và bằng hai lần tổng của n và m.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để 2 số hữu tỉ đều là dương :
\(\dfrac{m+2}{5}>0\Rightarrow m>-2\left(1\right)\)
\(\dfrac{m-5}{-6}>0\Rightarrow\dfrac{5-m}{6}>0\Rightarrow m< 5\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow-2< m< 5\Rightarrow m\in\left\{-1;0;1;2;3;4\right\}\left(m\in Z\right)\)

m + n = m.n => m = m.n - n = n(m - 1)
Thay m = n(m - 1) vào m + n = m: n ta có:
\(m+n=\frac{n\left(m-1\right)}{n}=m-1\)
=> m + n = m - 1=> m + n - m = -1 => n = -1
Ta có m +n = m.n => m + - 1 = - 1 .m => m - 1 = -m => m + m = 1 => 2m = 1 => m =1/2
Vậy n = -1 và m= 1/2

m + n = m.n => m = m.n - n = n(m - 1)
Thay m = n(m - 1) vào m + n = m: n ta có:
\(m+n=\frac{n\left(m-1\right)}{n}=m-1\)
=> m + n = m - 1=> m + n - m = -1 => n = -1
Ta có m +n = m.n => m + - 1 = - 1 .m => m - 1 = -m => m + m = 1 => 2m = 1 => m =1/2
Vậy n = -1 và m= 1/2

a: \(\dfrac{-8}{15}=\dfrac{-2}{15}+\dfrac{-6}{15}\)
\(\dfrac{-8}{15}=\dfrac{-1}{15}+\dfrac{-7}{15}\)
\(\dfrac{-8}{15}=\dfrac{-4}{15}+\dfrac{-4}{15}\)
b: \(-\dfrac{8}{15}=\dfrac{17}{15}-\dfrac{25}{15}\)
\(\dfrac{-8}{15}=\dfrac{9}{15}-\dfrac{17}{15}\)
\(\dfrac{-8}{15}=\dfrac{10}{15}-\dfrac{18}{15}\)
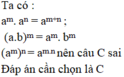
m = n = 0?
ko được