Từ điển M năm ngoài Ở vẽ hay tiếp tuyến MB,MC(B,C là hay tiếp điểm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 3 2023
a: góc MAO+góc MBO=90+90=180 độ
=>MAOB nội tiếp
ΔOCD cân tại O
mà OK là trung tuýen
nên OK vuông góc CD
Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại H
góc OHE+góc OKE=90+90=180 độ
=>OHEK nội tiếp
b: Xét ΔMAE và ΔMKA có
góc MAE=góc MKA
góc AME chung
=>ΔMAE đồng dạng với ΔMKA
=>MA/MK=ME/MA
=>MA^2=MK*ME=MC*MD
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 1
a. Câu này đơn giản em tự giải.
b.
Ta có: \(\left\{{}\begin{matrix}OB=OC=R\\MB=MC\left(\text{t/c hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OM\) là trung trực của BC
\(\Rightarrow OM\perp BC\) tại H đồng thời H là trung điểm BC hay \(HB=HC\)
\(OC\perp MC\) (MC là tiếp tuyến tại C) \(\Rightarrow\Delta OMC\) vuông tại C
Áp dụng hệ thức lượng trong tam giác vuông OMC với đường cao CH:
\(CH^2=OH.MH\)
c.
C nằm trên đường tròn và AB là đường kính \(\Rightarrow\widehat{ACB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=90^0\)
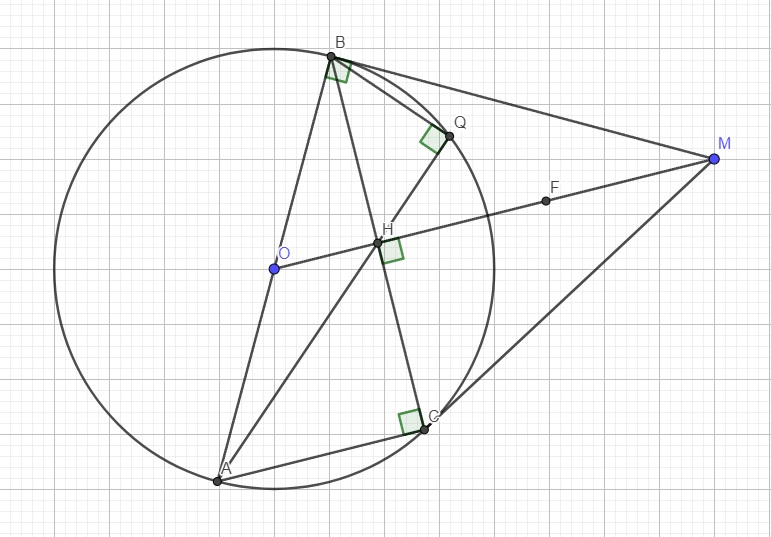
Xét hai tam giác MBH và BAC có:
\(\left\{{}\begin{matrix}\widehat{MHB}=\widehat{ACB}=90^0\\\widehat{MBH}=\widehat{BAC}\left(\text{cùng chắn BC}\right)\end{matrix}\right.\) \(\Rightarrow\Delta MBH\sim\Delta BAC\left(g.g\right)\)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{MH}{BC}\Rightarrow\dfrac{BH}{AC}=\dfrac{2HF}{2CH}\) (do F là trung điểm MH và H là trung điểm BC)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{HF}{CH}\)
Xét hai tam giác BHF và ACH có:
\(\left\{{}\begin{matrix}\dfrac{BH}{AC}=\dfrac{HF}{CH}\left(cmt\right)\\\widehat{BHF}=\widehat{ACH}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta BHF\sim\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{HBF}=\widehat{CAH}\)
Mà \(\widehat{CAH}=\widehat{CBQ}\) (cùng chắn CQ)
\(\Rightarrow\widehat{HBF}=\widehat{CBQ}\) hay \(\widehat{HBF}=\widehat{HBQ}\)
\(\Rightarrow B,Q,F\) thẳng hàng
7 tháng 3 2022
a: Xét tứ giác OEAM có \(\widehat{OEM}=\widehat{OAM}=90^0\)
nên OEAM là tứ giác nội tiếp
b: Xét ΔMAB và ΔMCA có
\(\widehat{MAB}=\widehat{MCA}\)
\(\widehat{AMB}\) chung
Do đó: ΔMAB\(\sim\)ΔMCA
Suy ra: MA/MC=MB/MA
hay \(MA^2=MB\cdot MC\)
6 tháng 2 2022
a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=180^0\)
nên MAOB là tứ giác nội tiếp
Xét (O) có
ΔADC nội tiếp
AC là đường kính
Do đó: ΔADC vuông tại D
Xét ΔCAM vuông tại A có AD là đường cao
nên \(AM^2=MB^2=MD\cdot MC\)
b: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
hay MO⊥AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2=MC\cdot MD\)
c/ OD vuông góc với MC
Đề bài yêu cầu gì?