chotam giac abc nhon co ab<ac ,trung tuyen am tren tia am lay d sao cho am=md ,e la diem doi xung voi a qua bc ,ha la giao cua ae va bc cm ae vuong goc voi ed
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
1 tháng 9 2017
Dựng đường cao BH.
Xét tam giác vuông CHB ta có .\(BC^2=BH^2+HC^2=BH^2+\left(AC-AH\right)^2\)
\(=BH^2+AH^2+AC^2-2AC.AH\)
Ta có \(AH=CB.\cos A\)
suy ra \(BC^2=BH^2+AH^2+AC^2-2AC.CB.\cos A\)
Hay \(BC^2=BA^2+AC^2-2AC.BC.\cos A\)
\(\Leftrightarrow a^2=b^2+c^2-2bc\cos A\)
MS
1
23 tháng 2 2023
a: Xét tư giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
Xét tứ giác CDHE có
góc CDH+góc CEH=180 độ
=>CDHE là tứ giác nội tiếp
b: CDHE là tứ giác nội tiếp
=>gó BED=góc FCB
góc FEH=góc BAD
mà góc FCB=góc BAD
nên góc BED=góc FEB
=>EB là phân giác của góc FED
c: góc IEO=góc IEH+góc OEH
=góc IHE+góc OBE
=góc BHD+góc CBH=90 độ
=>IE là tiếp tuyến của (O)
G
14 tháng 10 2017
Hình vẽ:
Giải:
Xét tam giác ABH và tam giác DBH, ta có:
\(\widehat{AHB}=\widehat{DHB}=90^0\)
\(HA=HD\left(gt\right)\)
HB là cạnh chung
\(\Rightarrow\Delta ABH=\Delta DBH\) (Hai cạnh góc vuông)
Lại xét tam giác ACH và tam giác DCH, ta có:
\(\widehat{AHC}=\widehat{DHC}=90^0\)
\(HA=HD\left(gt\right)\)
HC là cạnh chung
\(\Rightarrow\Delta ACH=\Delta DCH\) (Hai cạnh góc vuông)
Chúc bạn học tốt!
KV
15 tháng 3 2023
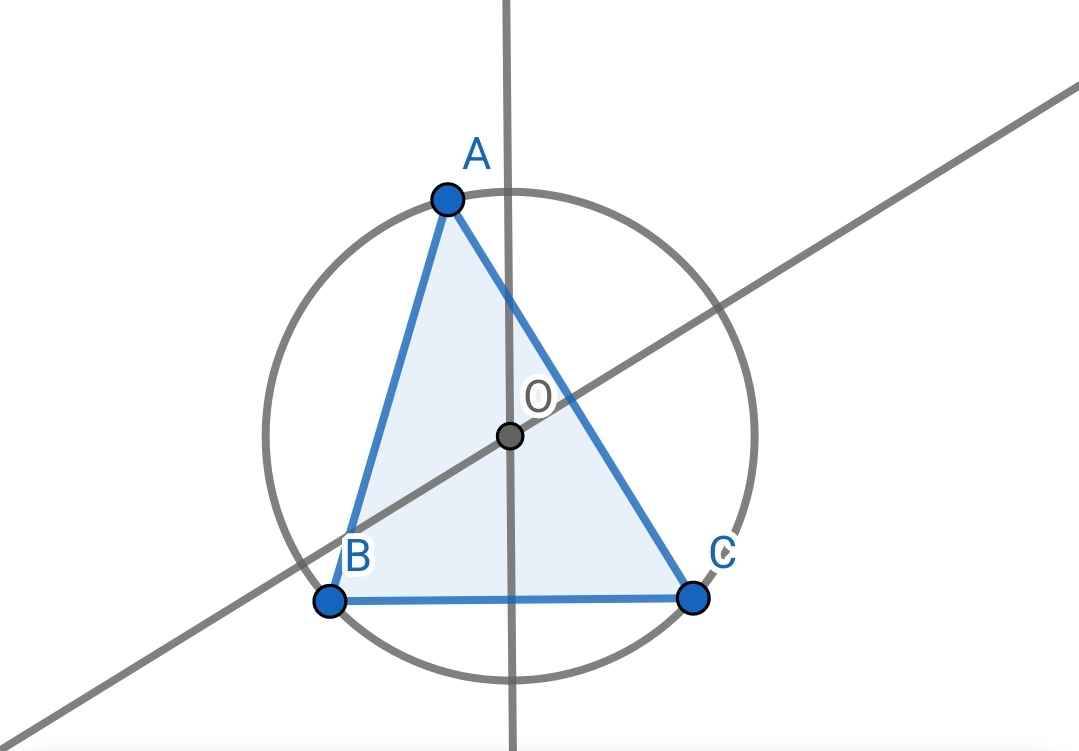
Vẽ hai đường trung trực của hai cạnh của tam giác
Gọi O là giao điểm của chúng
⇒ Tâm của đường tròn ngoại tiếp ∆ABC là O