Làm được câu nào thì làm nhé, mà làm hết thì tốt quá ạ:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4.
\(\lim\limits_{x\rightarrow8}f\left(x\right)=\lim\limits_{x\rightarrow8}\dfrac{\sqrt[3]{x}-2}{x-8}=\lim\limits_{x\rightarrow8}\dfrac{x-8}{\left(x-8\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\lim\limits_{x\rightarrow8}\dfrac{1}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}\)
\(=\dfrac{1}{4+4+4}=\dfrac{1}{12}\)
\(f\left(8\right)=3.8-20=4\)
\(\Rightarrow\lim\limits_{x\rightarrow8}f\left(x\right)\ne f\left(8\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=8\)
5.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-1+1-\sqrt[3]{1+3x}}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2x}{\sqrt[]{1+2x}+1}-\dfrac{3x}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{2}{\sqrt[]{1+2x}+1}-\dfrac{3}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)=\dfrac{2}{1+1}-\dfrac{3}{1+1+1}=0\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(3x^2-2x\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\) Hàm liên tục tại \(x=0\)
6.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{12}{1+1+1}=\dfrac{7}{2}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2-3x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)

a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)

a)
<=> \(3x-12x^2+12x^2-6x=9\)
<=> \(-3x=9\)
<=> \(x=-3\)
b)
<=> \(6x-24x^2-12x+24x^2=6\)
<=> \(-6x=6\)
<=> \(x=-1\)
c)
<=> \(6x-4-3x+6=1\)
<=> \(3x+2=1\)
<=> \(x=-\frac{1}{3}\)
d)
<=> \(9-6x^2+6x^2-3x=9\)
<=> \(-3x=0\)
<=> \(x=0\)
e) KO HIỂU ĐỀ
f)
<=> \(4x^2-8x+3-\left(4x^2+9x+2\right)=8\)
<=> \(-17x+1=8\)
<=> \(x=-\frac{7}{17}\)
g)
<=> \(-6x^2+x+1+6x^2-3x=9\)
<=> \(-2x=8\)
<=> \(x=-4\)
h)
<=> \(x^2-x+2x^2+5x-3=4\)
<=> \(3x^2+4x=7\)
<=> \(\orbr{\begin{cases}x=1\\x=-\frac{7}{3}\end{cases}}\)
a. \(3x\left(1-4x\right)+6x\left(2x-1\right)=9\)
\(\Rightarrow3x-12x^2+12x^2-6x=9\)
\(\Rightarrow-3x=9\)
\(\Rightarrow x=-3\)
b. \(3x\left(2-8x\right)-12x\left(1-2x\right)=6\)
\(\Rightarrow6x-24x^2-12x+24x^2=6\)
\(\Rightarrow-6x=6\)
\(\Rightarrow x=-1\)
c. \(2\left(3x-2\right)-3\left(x-2\right)=1\)
\(\Rightarrow6x-4-3x+6=1\)
\(\Rightarrow3x+2=1\)
\(\Rightarrow3x=-1\)
\(\Rightarrow x=-\frac{1}{3}\)

\(ac=-\dfrac{1}{2}< 0\Rightarrow\) pt luôn có 2 nghiệm phân biệt trái dấu
Do \(x_1< x_2\Rightarrow\left\{{}\begin{matrix}x_1< 0\\x_2>0\\\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left|x_1\right|=-x_1\\\left|x_2\right|=x_2\end{matrix}\right.\)
Đồng thời theo Viet: \(x_1+x_2=m\)
Ta có:
\(\left|x_2\right|-\left|x_1\right|=2021\)
\(\Leftrightarrow x_2-\left(-x_1\right)=2021\)
\(\Leftrightarrow x_1+x_2=2021\)
\(\Leftrightarrow m=2021\)

11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)

a) \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{98.99}+\frac{1}{99.100}\)\(=\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+...+\left(\frac{1}{98}-\frac{1}{99}\right)+\left(\frac{1}{99}-\frac{1}{100}\right)\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{98}-\frac{1}{99}+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}=\frac{99}{100}\)
b) \(\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{90}+\frac{1}{110}\)\(=\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{9.10}+\frac{1}{10.11}\)
\(=\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}...+\frac{1}{9}-\frac{1}{10}+\frac{1}{10}-\frac{1}{110}\)
\(=\frac{1}{2}-\frac{1}{100}=\frac{49}{100}\)
c) \(\frac{2}{11.13}+\frac{2}{13.15}+\frac{2}{15.17}+...+\frac{2}{97.99}\) \(=\frac{13-11}{11.13}+\frac{15-13}{13.15}+\frac{17-15}{15.17}+...+\frac{99-97}{97.99}\)
\(=\frac{1}{11}+\frac{1}{13}-\frac{1}{13}+\frac{1}{15}-\frac{1}{15}+\frac{1}{17}...+\frac{1}{97}-\frac{1}{99}\)
\(=\frac{1}{11}-\frac{1}{99}=\frac{8}{99}\)


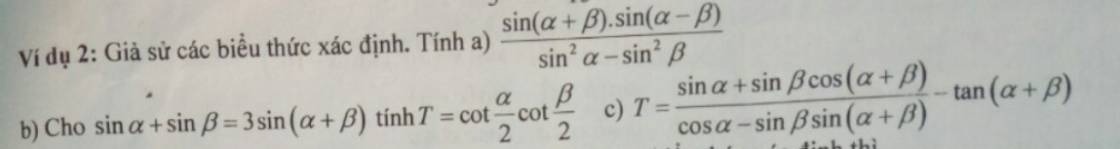
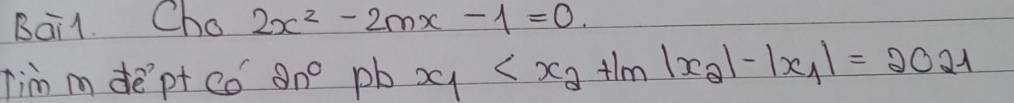



đề:)?