*Hãy vẽ ra:
+Hình thang.
+Hình bình hành.
+Hình chững nhật.
**Hãy chứng minh dâu hiệu nhận biết của cách hình đó.
Giúp mình với nha!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

em gửi bài qua fb thầy chữa cho, tìm fb của thầy bằng sđt nhé: 0975705122

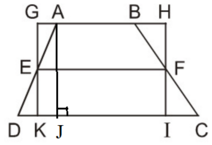
Ta có hình thang ABCD (AB // CD) với đường trung bình EF và hình chữ nhật GHIK như hình vẽ.
Dễ dàng chứng minh:
ΔAEG = ΔDEK, ΔBFH = ΔCFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên SABCD = SGHIK
Mà SGHIK = GH.GK= EF. AJ ( vì GH = EF, GK = AJ)
Nên SABCD = EF. AJ
Lại có:
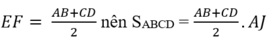
Vậy ta gặp lại công thức tính diện tích hình thang đã học nhưng bằng một phương pháp chứng minh khác.
Mặt khác, ta phát hiện công thức mới: Diện tích hình thang bằng tích của đường trung bình hình thang với đường cao.

Bạn tham khảo của google nhé, mk .... đuối ý bạn ạ. Dân chuyên văn mà ý nghĩ bay hết trơn rồi nên nhờ google :
* Hình thang cân :
Tính chất
- Hai cạnh bên bằng nhau
- Hai góc ở đáy bằng nhau
- Hai đường chéo bằng nhau
- Hình thang nội tiếp là hình thang cân.
Dấu hiệu nhận biết :
- Hình thang có hai góc kề một cạnh đấy bằng nhau là hình thang cân, Hình thang có hai đường chéo bằng nhau là hình thang cân.
- Hình thang có hai trục đối xứng của hai đáy trùng nhau là hình thang cân
- Hình thang có hai cạnh bên bằng nhau ( nếu hai cạnh bên ấy không song song ) là hình thang cân .
Mình biết tính chất với dấu hiệu nhận biết của hình thang cân rồi nhưng mình muốn biết thơ ạ

Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
∆AEG = ∆DEK;
∆BFH = ∆CFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà EF =
Do đó SABCD =
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.

Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
∆AEG = ∆DEK;
∆BFH = ∆CFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà EF =
Do đó SABCD =
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.

S hình vuông=cạnh x cạnh
S hình tròn=bán kính x bán kính x 3,14
S hình chữ nhật= Chiều dài x chiều rộng
S hình thoi=hai đường chéo x vs nhau rồi chia 2
S hình bình hành= cạnh đáy x chiều cao
S hinh thang=day be+ day lon roi nhan vs chieu cao roi chia cho 2
hình tròn S = 3,14 x R2 (R là bán kính)
hình chữ nhật : S = a x b ( với a, b là chiều dài và chiều rộng)
Hình thoi : S = a x b ( với a và b là hai đường chéo hình thoi
Hình bình hành S = a x h ( với a là cạnh hình bình hành và h là đường cao tương ứng với a)
+ vẽ hình e tự vẽ nha
+hình thang là hình có 2 cạnh đối song song vs nhau
+hình bình hành là hình có các cặp cạnh đối song song vs nhau
+hình chữ nhật là hình bình hành có 1 góc vuông
Chứng minh tứ giác có 3 góc vuông là hình chữ nhật
Chứng minh hình thang cân có 1 góc vuông là hình chữ nhật
Chứng minh hình bình hành có 1 góc vuông là hình chữ nhật
Chứng minh hình bình hành có 2 đường chéo là hình chữ nhật