Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Kẻ CE ⊥ AB, IH ⊥ AB, DF ⊥ AB
Suy ra: CE // DF // IH
IC = ID (gt)
Nên IH là đường trung bình của hình thang DCEF ⇒ IH = (DF + CE) / 2
Vì C là tâm hình vuông AMNP nên ∆ CAM vuông cân tại C
CE ⊥ AM ⇒ CE là đường trung tuyến (tính chất tam giác cân)
⇒ CE = 1/2 AM
Vì D là tâm hình vuông BMLK nên ∆ DBM vuông cân tại D
DF ⊥ BM ⇒ DF là đường trung tuyến (tính chất tam giác cân)
⇒ DF = 1/2 BM
Vậy CE + DF = 1/2 AM + 1/2 BM = 1/2 (AM + BM)= 1/2 AB = a/2
Suy ra: IH = (a/2) / 2 = a/4
a) Kẻ CE, IH, DF vuông góc với AB.
Ta chứng minh được
CE = \(\dfrac{AM}{2},\) DF = \(\dfrac{MB}{2},\)
CE + DF = \(\dfrac{AB}{2}=\dfrac{a}{2}\)
nên IH = \(\dfrac{a}{4}.\)
b) Khi điểm M di chuyển trên đoạn thẳng AB thì I di chuyển trên đoạn thẳng RS song song với AB và cách AB một khoảng bằng \(\dfrac{a}{4}\) (R là trung điểm của AQ, S là trung điểm của BQ, Q là giao điểm của BL và AN).
Gọi Q là giao điểm của BL và AN.
Ta có:
AN ⊥ MP (tính chất hình vuông)
BL ⊥ MK (tính chất hình vuông)
MP ⊥ MK (tính chất hình vuông)
Suy ra:
BL ⊥ AN ⇒ ∆ QAB vuông cân tại Q cố định.
M thayđổi thì I thay đổi luôn cách đoạn thẳng AB cố định một khoảng không đổi bằng a/4 nên I chuyển động trênđường thẳng song song với AB, cách AB một khoảng bằng a/4.
Khi M trùng B thì I trùng với S là trung điểm của BQ.
Khi M trùng với A thì I trùng với R là trung điểm của AQ.
Vậy khi M chuyển động trên đoạn AB thì I chuyển động trên đoạn thẳng RS song song với AB, cách AB một khoảng bằng a/4
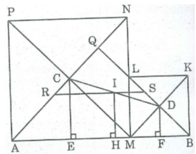
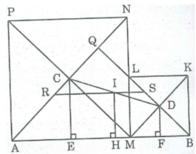
a. Kẻ \(CE\perp AM;DG\perp MB\) , ta thấy ngay CE = EM; DG = GM (Do AMNP, BMLKA là hình vuông)
Từ I kẻ IJ // CE // DG : IJ là đường trung bình hình thang CEGD. Vậy thì
\(IJ=\frac{EC+DG}{2}=\frac{EM+MG}{2}=\frac{AB}{4}=\frac{a}{4}.\)
Do \(IJ\perp AB\) nên khoảng cách từ I tới AB là IJ = \(\frac{a}{4}.\)
b. Do khoảng cách từ I tới AB không thay đổi nên khi M di chuyển trên AB thì I di chuyển trên đường thẳng song song AB, cách AB một khoảng bằng \(\frac{a}{4}.\)
Bài của mình giống cô giáo :
Câu hỏi của Nguyễn Minh Phương - Toán lớp 8 - Học toán với OnlineMath
Cậu tahm khảo bài của cô nha