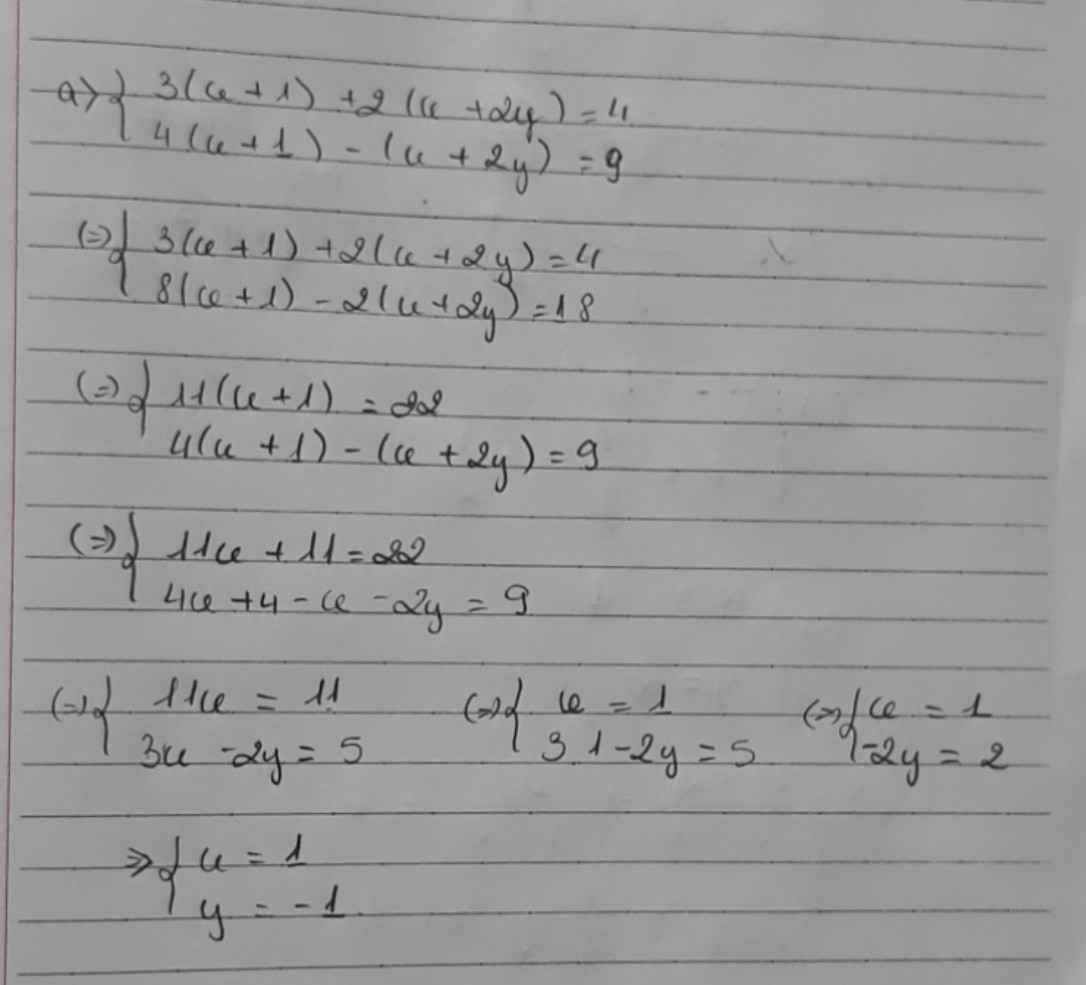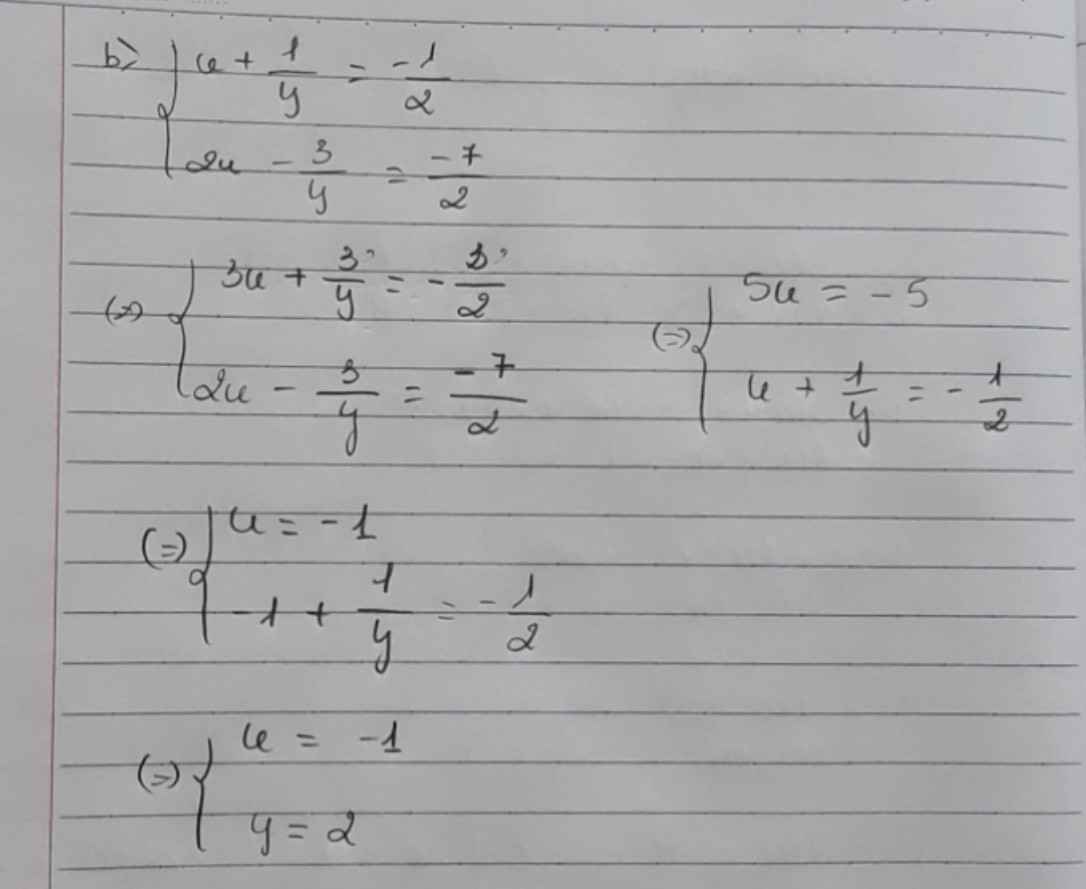- Rút gọn A=\(\frac{x^2-x+2}{x^2}\)\(\div\sqrt{\frac{x^4+4}{x^2}+6\left(\frac{x^2+2}{x}\right)^2-15}\) với x\(\ne0\)
- Cho a, b, c thỏa mãn \(\hept{\begin{cases}a+b+c=1\\a^2+b^2+c^2=1\\a^3+b^3+c^3=1\end{cases}}\). Chứng minh \(a^{2015}+b^{2015}+c^{2015}=1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 7 2021
c) Ta có: \(\left\{{}\begin{matrix}\dfrac{x+2}{x+1}+\dfrac{2}{y-2}=6\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x+1}+\dfrac{10}{y-2}=25\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{11}{y-2}=22\\\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-2=\dfrac{1}{2}\\\dfrac{1}{x+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=1\\y-2=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{5}{2}\end{matrix}\right.\)
18 tháng 10 2020
a) \(\Leftrightarrow\hept{\begin{cases}\frac{x+1+1}{x+1}+\frac{2}{y-2}=6\\\frac{5}{x+1}-\frac{1}{y-2}=3\end{cases}\Leftrightarrow\hept{\begin{cases}1+\frac{1}{x+1}+\frac{2}{y-2}=6\\\frac{5}{x+1}-\frac{1}{y-2}=3\end{cases}}}\)
Đặt \(a=\frac{1}{x+1};b=\frac{1}{y-2}\)
\(\Leftrightarrow\hept{\begin{cases}1+a+2b=6\\5a-b=3\end{cases}\Leftrightarrow\hept{\begin{cases}a+2b=5\\5a-b=3\end{cases}\Leftrightarrow}\hept{\begin{cases}a=1\\b=2\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{1}{x+1}=1\\\frac{1}{y-2}=2\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=\frac{5}{2}\end{cases}}}\)
b) ĐK: \(\hept{\begin{cases}x\ne0\\y\ne1\end{cases}}\)
\(PT\left(1\right)\Leftrightarrow\left(x^2-2x\right)\left(x^2-2x+4\right)=0\Leftrightarrow x\left(x-2\right)\left(x^2-2x+4\right)=0\Leftrightarrow x=0\)(loại)
, x=2 , x2-2x+4=0 (3)
pt(3) vô nghiệm vì \(\Delta'=1-4=-3< 0\)
Thay x=2 vào pt(2) ta được \(\frac{1}{2}+\frac{1}{y-2}=\frac{3}{2}\Leftrightarrow\frac{1}{y-1}=1\Leftrightarrow y-1=1\Leftrightarrow y=2\left(tm\text{đ}k\right)\)
Vậy nghiệm của hpt là: (x;y)=(2;2)
18 tháng 7 2021
a) \(\hept{\begin{cases}3\left(x+1\right)+2\left(x+2y\right)=4\\4\left(x+1\right)-\left(x+2y\right)=9\end{cases}}\Leftrightarrow\hept{\begin{cases}3\left(x+1\right)+2\left(x+2y\right)=4\\8\left(x+1\right)-2\left(x+2y\right)=18\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}11\left(x+1\right)=22\\3\left(x+1\right)+2\left(x+2y\right)=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\4y+8=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=-1\end{cases}}\)
18 tháng 7 2021
b) ĐK : y khác 0
\(\hept{\begin{cases}x+\frac{1}{y}=-\frac{1}{2}\\2x-\frac{3}{y}=-\frac{7}{2}\end{cases}}\Leftrightarrow\hept{\begin{cases}3x+\frac{3}{y}=-\frac{3}{2}\\2x-\frac{3}{y}=-\frac{7}{2}\end{cases}}\Leftrightarrow\hept{\begin{cases}5x=-5\\3x+\frac{3}{y}=-\frac{3}{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=-1\\-3+\frac{3}{y}=-\frac{3}{2}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\\frac{3}{y}=\frac{3}{2}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=2\left(tm\right)\end{cases}}\)
29 tháng 5 2018
4. Ta có: \(a+b+c=6abc\)
\(\Rightarrow\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}=6\)
Đặt \(\frac{1}{a}=x;\frac{1}{b}=y;\frac{1}{c}=z\)
\(\Rightarrow xy+yz+zx=6\)
Lại có: \(\frac{bc}{a^3\left(c+2b\right)}=\frac{1}{a^3\frac{c+2b}{bc}}=\frac{\frac{1}{a^3}}{\frac{1}{b}+\frac{2}{c}}=\frac{x^3}{y+2z}\)
Tương tự suy ra:
\(S=\frac{x^3}{y+2z}+\frac{y^3}{z+2x}+\frac{z^3}{x+2y}\)
\(=\frac{x^4}{xy+2zx}+\frac{y^4}{yz+2xy}+\frac{z^4}{zx+2yz}\)
\(\ge\frac{\left(x^2+y^2+z^2\right)^2}{3\left(xy+yz+zx\right)}\ge\frac{x^2+y^2+z^2}{3}\ge\frac{xy+yz+zx}{3}=2\)
Dấu = xảy ra khi \(x=y=z=\sqrt{2}\Rightarrow a=b=c=\frac{1}{\sqrt{2}}\)