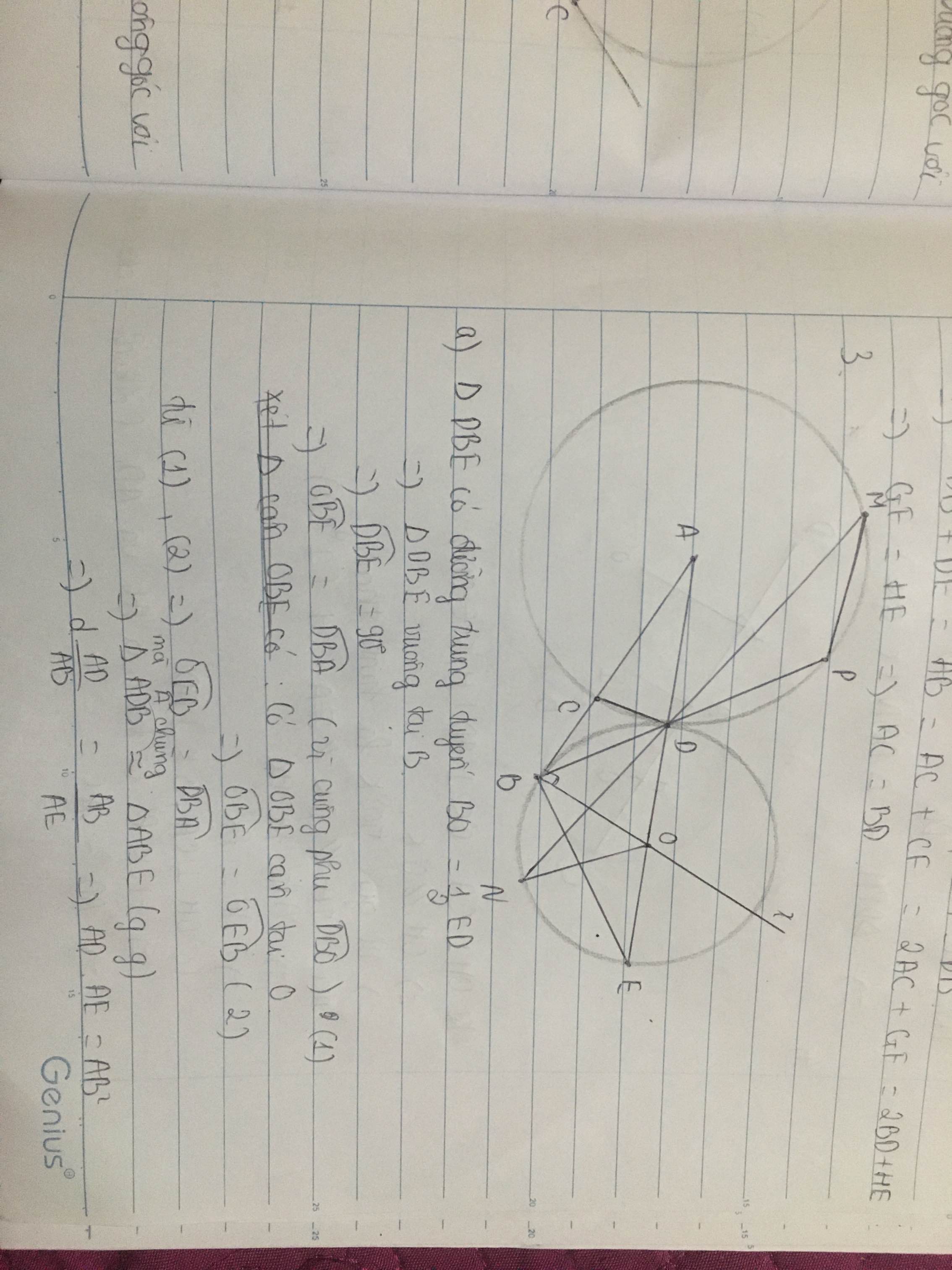
Cho đoạn thẳng AB. Kẻ tia Bx vuông góc với AB. Trên Bx lấy một điểm O sao cho BO = $\frac{1}{2}$ AB. Tia AO cắt đường tròn (O ; OB) ở D và E (D nằm giữa A và O). Đường tròn (A ; AD) cắt AB ở C.
a) Chứng minh $DE^2=AD.AE$.
b) Chứng minh $AC^2=CB.AB$.
c) Tia BD cắt đường tròn (A) ở P. Một đường thẳng đi qua D cắt đường tròn (A) ở M và cắt đường tròn (O) ở N. Chứng minh $\Delta DPM \backsim \Delta DBN$.