chứng minh trong tam giác,đối diện với cạnh lớn hơn là góc lớn hơn, đối diện với góc lớn hơn là cạnh lớn hơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
1
9 tháng 3 2017
Giả sử ∆ABC có AB < AC . Lấy điểm D trên cạnh AC ( D nằm giữa A và C ) sao cho AB = AD
Kẻ tia phân giác của ∠A cắt BC tại E , nối E với D
Xét ∆ABE và ∆ADE có :
AB = AC (cạnh dựng)
∠A1 = ∠A2 (AE là phân giác của ∠BAC)
AE là cạnh chung
=> ∆ABE = ∆ADE (c - g - c)
=> ∠B = ∠ADE (góc T/Ư)
∠ADE là góc ngoài của ∆DEC => ∠ADE = ∠DEC + ∠C => ∠ADE > ∠C
Mà ∠B = ∠ADE => ∠B > ∠C
Vậy ∆ABC có AB < AC thì ∠C < ∠B hoặc ∠C < ∠B thì AB < AC
Hay trong tam giác cạnh đối diện với góc lớn hơn thì lớn hơn
CM
22 tháng 2 2018
Nếu AB > AC thì ∠C > ∠B (góc đối diện với cạnh lớn hơn là góc lớn hơn)
Điều này trái với giả thiết ∠B > ∠C nên không xảy ra.
CM
28 tháng 5 2017
Nếu AB = AC thì ΔABC cân tại A
⇒ ∠B = ∠C(tính chất tam giác cân)
Điều này trái với giả thiết ∠B > ∠C nên không xảy ra.
Vậy nếu ∠B > ∠C thì AC > AB.
17 tháng 9 2023
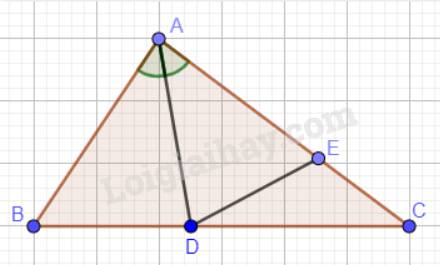
a) Xét hai tam giác ABD và AED: AB = AE, AD chung, \(\widehat {BAD} = \widehat {EAD}\)(AD là phân giác của góc BAC).
Vậy \(\Delta ABD = \Delta AED\) (c.g.c)
b) Ta có: \(\Delta ABD = \Delta AED \Rightarrow \widehat {ABD} = \widehat {AED}\) (2 góc tương ứng)
Ba điểm A, E, C thẳng hàng nên \(\widehat {AED} = 180^\circ \).
Vậy \(\widehat {ABD} = \widehat {AED} = 180^\circ - \widehat {DEC} = \widehat {EDC} + \widehat {ECD}\)(Tổng ba góc trong tam giác EDC bằng 180°).
Do đó, góc B bằng tổng của góc EDC và góc C. Vậy \(\widehat B > \widehat C\).
PT
1
6 tháng 3 2019
T làm, sai đâu sửa hộ nhé
Giả sử có tam giác ABC có góc B > góc C => AC < AB
Ta xét 2 trường hợp:
TH1: Nếu AB > AC thì góc B < góc C (góc đối diện với cạnh lớn hơn là góc lớn hơn)
Điều này trái với giả thuyết góc B > góc C
TH2: Nếu AB = AC thì tam giác ABC cân tại A
=> Góc B = góc C (tính chất của tam giác cân)
Điều này trái với giả thuyết góc B > góc C
Vậy: Góc B > góc C => AC < AB (đpcm)