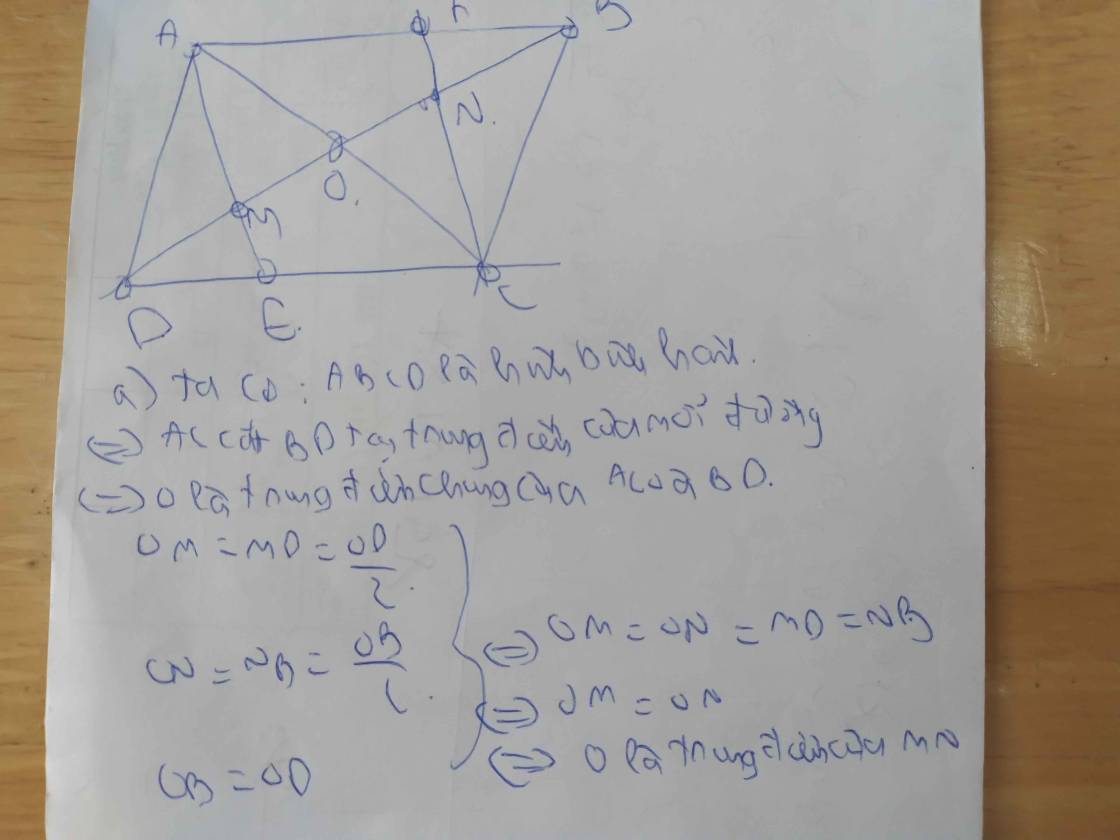
Cho hbh ABCD, O là giao điểm hai đường chéo. Lấy E trên OD và F trên OB, sao cho OE=OF. Gọi M là giao điểm AE và CD. Điểm E nằm ở đâu thì DM = MC:2 ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 6 2016
vì O là giao điểm 2 đường chéo AC và BD của hbh ABCD nên O, là trung điểm AC và BD
=> OA=OC (1)
ta có AE = FC (GT) (2)
trừ theo vế của (1) và (2) ta được
OA-AE = OC - FC
OE = OF => O là trung điểm EF
xét tứ giác EBFD có O là trung điểm đường chéo BD, O là trung điểm đường chéo EF => EBFD là hbh
8 tháng 8 2016
Bài 1:
Xét ΔADE và ΔCBF có:
AD=BC(gt)
\(\widehat{ADE}=\widehat{CBF}\) (soletrong do AD//BC)
DE=BF(gt)
=>ΔADE=ΔCBF(c.g.c)
=>AE=CF (1)
Xét ΔABF và ΔCDE có:
BF=DE(gt)
\(\widehat{ABF}=\widehat{CDE}\) (soletrong do AB..CD)
AB=CD(gt)
=>ΔABF=ΔCDE(c.g.c)
=>AF=CE (2)
Từ (1)(2) suy ra: AFCE là hbh
=>AF//CE
8 tháng 8 2016
XIN LỖI NẾU LM PHIỀN CÁC BN MK ĐANG CẦN GẤP GIẢI GIÙM NHÉ 
9 tháng 11 2015
Tự vẽ hình nha
a) tam giác OEA = tam giác OFC (c-g-c)
=>A=C mà 2 góc này là SLT => AE//CF
b)Kẻ OK song song với CF hay EI
Vì DE=EO=OF ;EI//OK//FC
=> EI;OK;FC là 3 dường thẳng // cách đều
=> DI=IK=KC => dpcm
Tích nhé bạn