Tam giác ABC vuông tại A.Tia phân giác của góc ABC cắt cạnh AC tại D.Kẻ DE vuông góc Bc tại E
a)cm:Tam giác ABD=Tam Giác EBD Và tam giác BAE Cân
b)Tia ED cắt BA tại F.cm:DE<DF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
18 tháng 6 2023
Đúng(0)
Những câu hỏi liên quan
18 tháng 6 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
=>DF=DC>DE
30 tháng 3 2021
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)
TI
30 tháng 3 2021
a) xét tam giác ABD và tam giác EBD vuông tại A, E ( gt, DE⊥BC)
BD chung
góc ABD = góc EBD ( BD là tia p/g của góc B)
do đó : tam giác ABD = tam giác EBD ( cạnh huyền + góc nhọn )
15 tháng 3 2022
1: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
2: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: AF=EC
Xét ΔBFC có BA/AF=BE/EC
nên AE//FC
8 tháng 3 2023
`a)`
+, `Delta ABC` vuông tại `A(GT)=>hat(A)=90^0`
`DE⊥BC(GT)=>hat(BED)=90^0`
`BD` là p/g của `hat(ABC)(GT)=>hat(B_1)=hat(B_2)`
Xét `Delta ABD` và `Delta EBD` có :
`{:(hat(A)=hat(BED)(=90^0)),(BD-chung),(hat(B_1)=hat(B_2)(cmt)):}}`
`=>Delta ABD=Delta EBD(c.h-g.n)(đpcm)`
+, Có `Delta ABD=Delta EBD(cmt)`
`=>BA=BE` ( 2 cạnh t/ứng ) `(đpcm)`
`b)`
Có `BA=BE(cmt)`
`=>Delta ABE` cân tại `B`
mà `hat(ABE)=60^0(hat(ABC)=60^0)`
nên `Delta ABC` đều `(đpcm)`
`c)`
Có `Delta ABC` vuông tại `A=>hat(ABC)+hat(C)=90^0`
hay `60^0+hat(C)=90^0`
`=>hat(C)=90^0-60^0=30^0` (1)
`Delta ABE` đều `(cmt)=>hat(A_1)=60^0`
`=>hat(A_2)=30^0` (2)
Từ `(1)` và `(2)=>Delta EAC` cân tại `E`
`=>AE=EC`
Có `Delta ABE` đều `(cmt)=>AB=AE`
mà `AE=EC(cmt)`
`{:(nên EC=AB),(mà AB=EB(cmt);AB=5cm):}}`
`=>EC=EB=5cm`
Vậy `BC=EC+EB=5+5=10(cm)`
7 tháng 3 2023
a: Xet ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE
b: BA=BE và góc ABE=60 độ
=>ΔBAE đều
c: Xét ΔABC vuông tại A có cos B=AB/BC
=>5/BC=1/2
=>CB=10cm
16 tháng 4 2023
\(\text{#TNam}\)
`a,` Xét Tam giác `ABD` và Tam giác `EBD` có:
`\text {BD chung}`
\(\widehat{ABD}=\widehat{EBD} (\text {tia phân giác}\)\(\widehat{BAE})\)
`=> \text {Tam giác ABD = Tam giác EBD (ch-gn)}`
`b,`
Vì Tam giác `ABD =` Tam giác `EBD (a)`
`-> BA = BE (\text {2 cạnh tương ứng})`
Xét Tam giác `BAC` và Tam giác `BEF` có:
\(\widehat{B}\) \(\text {chung}\)
`BA = BE (CMT)`
\(\widehat{BAC}=\widehat{BEF}=90^0\)
`=> \text {Tam giác BAC = Tam giác BEF (g-c-g)}`
`-> BF = BC (\text {2 cạnh tương ứng})`
Gọi `I` là giao điểm của `BD` và `CF`
Xét Tam giác `BIF` và Tam giác `BIC` có:
`BF = BC (CMT)`
\(\widehat{FBI}=\widehat{CBI} (\text {tia phân giác}\) \(\widehat{FBC})\)
\(\text {BI chung}\)
`=> \text {Tam giác BIF = Tam giác BIC (c-g-c)}`
`->`\(\widehat{BIF}=\widehat{BIC} (\text {2 góc tương ứng})\)
Mà `2` gióc này nằm ở vị trí kề bù
`->`\(\widehat{BIF}+\widehat{BIC}=180^0\)
`->`\(\widehat{BIF}=\widehat{BIC}=\)`180/2=90^0`
`-> \text {BI} \bot \text {FC}`
`-> \text {BD}` `\bot` `\text {FC (đpcm)}`
30 tháng 4 2022
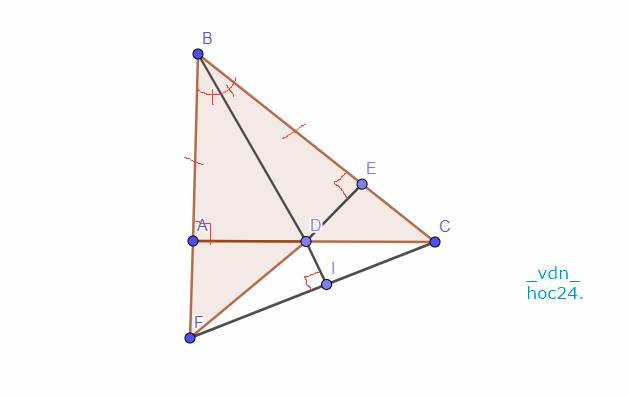
a: XétΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó:ΔBAD=ΔBED
Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
hay ΔDFC cân tại D
b: Ta có: DE=DA
mà DA<DF
nên DE<DF
