Cho hình thang MNPQ có đáy nhỏ MN=4cm, đáy lớn PQ= 6cm . Khi đó độ dài đường trung bình của hình thang MNPQ là... cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 11 2016
đường trung bình hình thang MNPQ = (6+4):2 = 5 (cm)
mik nha chế
13 tháng 10 2016
Ta có : GỌi dộ dài đường trung bình là EF
=> EF=(MN+PQ):2=(4+6):2=10:2=5
12 tháng 1 2023
PQ=7*2=14cm
\(S_{MNPQ}=\dfrac{1}{2}\cdot\left(7+14\right)\cdot4=2\cdot21=42\left(cm^2\right)\)
CM
5 tháng 10 2017
Đáp án cần chọn là: C
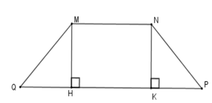
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 12 cm nên QH = KP = 40 − 12 2 = 14 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 12 + 40 ) .14 2 = 364 c m 2
CM
21 tháng 2 2018
Đáp án cần chọn là: B
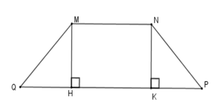
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 8 cm nên QH = KP = 30 − 8 2 = 8 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 8 + 30 ) .11 2 = 209 c m 2 .
AH
Akai Haruma
Giáo viên
10 tháng 5 2021
Lời giải:
$S_{MNQ}=S_{MNP}$ (do chiều cao bằng nhau và chung đáy)
$\Rightarrow S_{MQK}=S_{NKP}=15$ (cm2)
Kẻ đường cao $NH$ xuống $MP$, đường cao $QT$ xuông $MH$
\(\frac{S_{MNP}}{S_{MQP}}=\frac{MN}{PQ}=\frac{3}{5}\)
\(\frac{S_{MNP}}{S_{MQP}}=\frac{NH}{QT}\)
\(1=\frac{S_{NPK}}{S_{MQK}}=\frac{NH\times PK}{QT\times MK}\Rightarrow \frac{NH}{QT}=\frac{MK}{PK}\)
Từ 3 điều trên suy ra $\frac{MK}{PK}=\frac{3}{5}$
$\frac{S_{MNK}}{S_{NPK}}=\frac{MK}{PK}=\frac{3}{5}$
$S_{MNK}=\frac{3}{5}\times S_{NPK}=\frac{3}{5}\times 15=9$ (cm2)
$\frac{S_{MQK}}{S_{PQK}}=\frac{MK}{PK}=\frac{3}{5}$
$\Rightarrow S_{PQK}=\frac{5}{3}\times S_{MQK}=\frac{5}{3}\times 15=25$ (cm2)
Diện tích hình thang:
$15+15+9+25=64$ (cm2)
5 tháng 10 2021
\(\overrightarrow{EM}+\overrightarrow{EN}+\overrightarrow{EP}+\overrightarrow{EQ}\)
\(=\overrightarrow{EN}+\overrightarrow{EQ}\)(1)
\(\overrightarrow{PN}+\overrightarrow{MQ}\)
\(=\overrightarrow{PE}+\overrightarrow{EN}+\overrightarrow{ME}+\overrightarrow{EQ}\)
\(=\overrightarrow{EN}+\overrightarrow{EQ}\)(2)
Từ (1) và (2) suy ra \(\overrightarrow{EM}+\overrightarrow{EN}+\overrightarrow{EP}+\overrightarrow{EQ}=\overrightarrow{PN}+\overrightarrow{MQ}\)