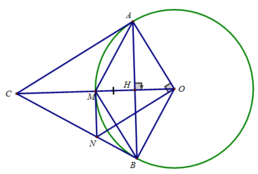
Cho2 đường tròn (O) và (O') cắt nhay tại A và B. đường thẳng OO' cắt đường tròn (O) tại C và (O') tại B. vẽ tiếp tuyến chung MN của 2 đường tròn (M thuộc O, N thuộc O') hai đường thẳng cắt nhau tại E
- Chứng minh tứ giác CMND nội têếp
- Gọi K là giao điểm của AB và MN.chứng minh KM=KN
- chứng minh CM,DN,AB đồng qui