Bài 2: Cho cân tại là trung điểm của thuộc sao cho . Chứng minh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho ∆ABC, kẻ đường cao AH trên tia đối tia HA lấy điểm M sao cho H là trung điểm của AM
a) Chứng minh ∆ABM cân
b) Chứng minh ∆ABC=∆MBC
a, Vì AH vuông góc BC ( gt )
=> BH vuông góc AM
Xét tam giác ABM có BH vừa là đường cao , vừa là trung tuyến
=> tam giác ABM cân tại B
b, Lại có : AH vuông góc BC
=> CH vuông góc AM
Xét tam giác ACM có CH vừa là đường cao , vừa là trung tuyến
=> tam giác ACM cân tại C
Xét tam giác ABC và tam giác MBC có :
BC chung
AB = MB ( tam giác ABM cân tại B )
AC = CM ( tam giác ACM cân tại C )
=> tam giác ABC = tam giác MBC ( c.c.c )

c) Ta có: MH//AB(cmt)
nên EH//AB
Suy ra: \(\widehat{CHE}=\widehat{CBA}\)(hai góc đồng vị)
mà \(\widehat{CBA}=\widehat{HCE}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{EHC}=\widehat{ECH}\)
Xét ΔEHC có \(\widehat{EHC}=\widehat{ECH}\)(cmt)
nên ΔEHC cân tại E(Định lí đảo của tam giác cân)
Ta có: \(\widehat{ECH}+\widehat{EAH}=90^0\)(ΔAHC vuông tại H)
\(\widehat{EHC}+\widehat{AHE}=90^0\)(HE là tia nằm giữa hai tia HC,HA)
mà \(\widehat{EHC}=\widehat{ECH}\)(cmt)
nên \(\widehat{EAH}=\widehat{EHA}\)
Xét ΔEHA có \(\widehat{EAH}=\widehat{EHA}\)(cmt)
nên ΔEHA cân tại E(Định lí đảo của tam giác cân)
Ta có: EH=EC(ΔEHC cân tại E)
mà EH=EA(ΔEHA cân tại E)
nên EC=EA
hay E là trung điểm của AC(Đpcm)
a) Xét ΔAIH và ΔMIB có
IA=IM(gt)
\(\widehat{AIH}=\widehat{MIB}\)(hai góc đối đỉnh)
IH=IB(I là trung điểm của BH)
Do đó: ΔAIH=ΔMIB(c-g-c)
Suy ra: AH=MB(hai cạnh tương ứng)
Xét ΔBMA có
AB+BM>AM(Bđt tam giác)
mà AH=MB(cmt)
nên AB+AH>AM(Đpcm)
b) Xét ΔBIA và ΔHIM có
IA=IM(gt)
\(\widehat{BIA}=\widehat{HIM}\)(hai góc đối đỉnh)
IB=IH(I là trung điểm của BH)
Do đó: ΔBIA=ΔHIM(c-g-c)
Suy ra: \(\widehat{IBA}=\widehat{IHM}\)(hai góc tương ứng)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//MH(Dấu hiệu nhận biết hai đường thẳng song song)

a: Xét ΔAMB và ΔNMC có
MA=MN
góc AMB=góc NMC
MB=MC
Do đó: ΔAMB=ΔNMC
b: Xét ΔBAI có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAI cân tại B
=>BA=BI=CN

Tham khảo
a) Xét ΔAMH và ΔNMB có:
+ AM = NM
+ góc AMH = góc NMB (đối đỉnh)
+ MH = MB
=> ΔAMH = ΔNMB (c-g-c)
=> góc MAH = góc MNB
=> AH//BN
Mà AH vuông góc BC
=> BN vuông góc BC
b) Do ΔAMH = ΔNMB
=> AH = BN
Trong tam giác vuông ABH vuông tại H
=> AB > AH (cạnh huyền là cạnh lớn nhất)
=> AB > BN
c) Ta cm được ΔABM = ΔNHM (c-g-c)
=> góc BAM = góc HNM
Trong ΔANH có:NH > AH
=> góc MAH > góc MNH
=> góc MAH > góc BAM
d) Ta cm được ΔABH = ΔACH (ch-cgv)
=> BH = CH
=> CH = 2. HM
Tam giác ANC có CM là đường trung tuyến (do M là trung điểm của AN)
và CH/CM =2/3
=> H là trọng tâm của ΔANC
=> AH là đường trung tuyến
=>AH đi qua trung điểm của CN
hay A,H,I thẳng hàng

a) Xét ΔABN và ΔACM có
AB=AC(ΔABC cân tại A)
\(\widehat{BAN}\) chung
AN=AM(gt)
Do đó: ΔABN=ΔACM(c-g-c)
Suy ra: BN=CM(hai cạnh tương ứng)
b) Xét ΔAHB và ΔAHC có
AB=AC(ΔABC cân tại A)
AH chung
HB=HC(H là trung điểm của BC)
Do đó: ΔAHB=ΔAHC(c-c-c)
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)(hai góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
hay AH⊥BC(đpcm)
c) Ta có: AH⊥BC(cmt)
mà H là trung điểm của BC(gt)
nên AH là đường trung trực của BC
⇔EH là đường trung trực của BC
⇔EB=EC(Tính chất đường trung trực của một đoạn thẳng)
Xét ΔEBC có EB=EC(cmt)
nên ΔEBC cân tại E(Định nghĩa tam giác cân)

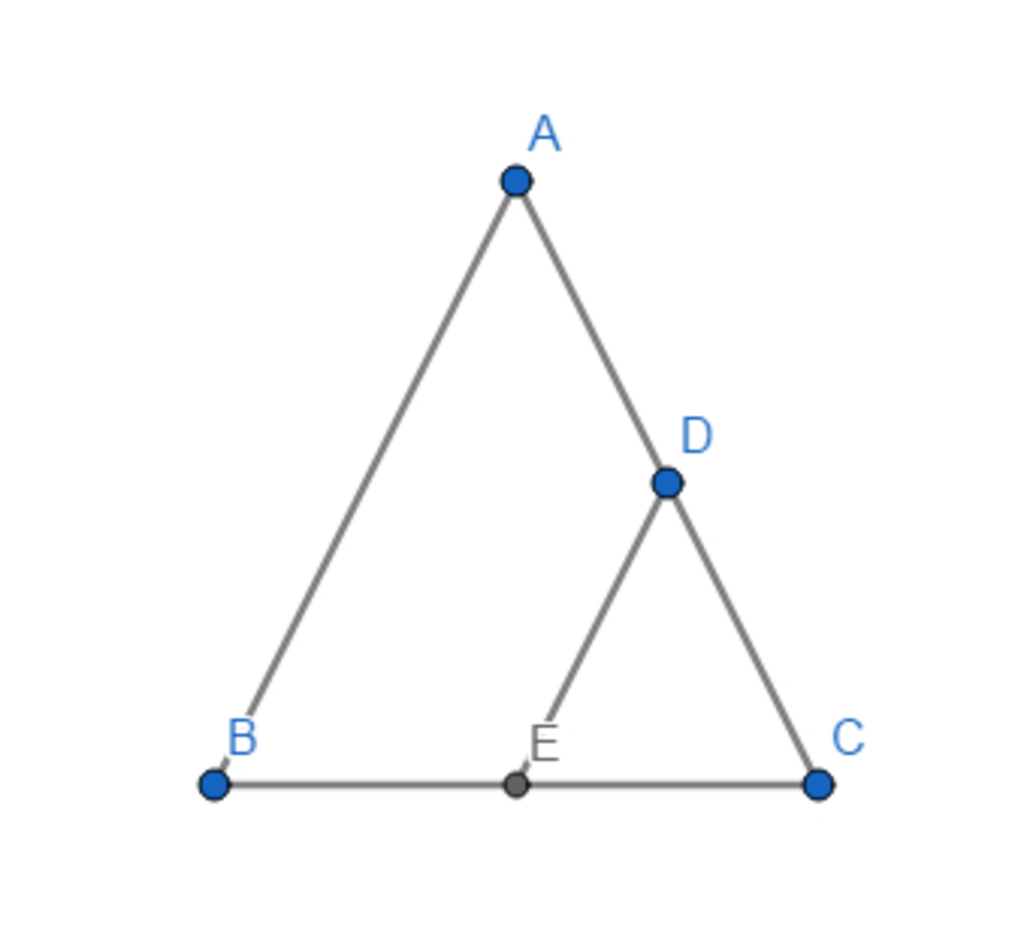
a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{HCB}=\widehat{HBC}\)
hay ΔHBC cân tại H
=>HB=HC
mà AB=AC
nên AH là đường trung trực của BC
=>A,H,M thẳng hàng
b: BC=16cm nên BM=CM=8cm
=>AM=6cm
a. Nối AM
Xét \(2\Delta:\Delta AMB\) và \(\Delta AMC\) có:
\(\left\{{}\begin{matrix}AM.chung\\AB=AC\left(gt\right)\\BM=BC\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}\)
Mà: \(\widehat{BMC}=180^o\)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=90^o\)
\(\Rightarrow AM.là.đường.cao\)
Mà H là giao của BD và CE
Vậy H là trực tâm của tam giác ABC
Vậy AH đi qua M
b. \(MC=16:2=8\left(cm\right)\)
Áp dụng định lý Pi - ta - go, suy ra:
\(AM^2+MC^2=AC^2\)
\(\Leftrightarrow AH=\sqrt{AC^2-MC^2}=\sqrt{10^2-8^2}=6\left(cm\right)\)

a) Vì ∆ABC cân tại A có AH là đường cao nên AH cũng là đường trung tuyến
Suy ra BH=CH
Xét ∆AHB và ∆AHC có
AH là cạnh chung
BH=CH (cmt)
AB=AC (∆ABC cân tại A)
Do đó ∆AHB=∆AHC
Xét ∆AMH ta có
AD vuông góc với MH (HD vuông góc AB)
Suy ra AD là đường cao của ∆AMH (1)
DH=DM (gt)
Nên AD là đường trung bình của ∆AMH (2)
Từ (1) và (2) suy ra ∆AMH cân tại A
Suy ra AM=AH

a,Ta có:
\(AH\perp BC\) nên \(\widehat{AHB}\) +90 độ.
Vì M là tia đối của HA nên \(\widehat{MHB}\)= 90 độ.
Xét \(\Delta ABH\) và \(\Delta MBH\)có
AH = MH (gt)
\(\widehat{AHB}\) = \(\widehat{MHB}\) (= 90 độ )
BH : cạnh chung
\(\Rightarrow\Delta ABH=\Delta MBH\)( c.g.c )
b,Xét \(\Delta AHCv\text{à}\Delta MHC\)Ta có:
AH = HM (gt)
\(\widehat{AHC}\)= \(\widehat{MHC}\)(= 90 độ)
HC : cạnh chung
\(\Rightarrow\Delta AHC=\Delta MHC\)( c.g.c)
\(\Rightarrow\)AC=CM ( t/ứ)
Mà AC = CN (gt) và CM = AC (cmt)
nên CM = CN
\(\Rightarrow\Delta CMN\)cân
Giả sử \(M\)nằm giữa \(H\)và \(C\).
Tam giác \(AHM\)vuông tại \(H\)suy ra \(\widehat{AMH}< 90^o\Leftrightarrow\widehat{AMC}>90^o\).
Xét tam giác \(AMC\)có: \(\widehat{AMC}>90^o>\widehat{ACM}\Leftrightarrow AC>AM\).